一維δ函式
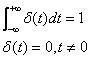二維δ函式 也可叫做衝擊函式。它使用極限語言來定義的一種特殊的函式。δ函式的最常用定義方式為： 形象的說得話就是一個寬度趨近於零而高度趨近於無窮的矩形，其面積為1.
二維δ函式
通過上面一維δ函式的定義，我們來延伸到二維空間來。二維δ函式的定義有著與一維相似的定義方式：
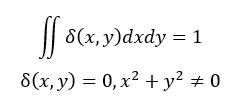二維δ函式 此時形象的說法就是：空間中的一個長方體。當起地面面積趨於0，長方體的高趨於無窮時，而長方體的體積為1.
二維δ函式 二維δ函式 
二維δ函式是從一維δ函式延伸而來，形象的說法就是：空間中的一個長方體。當起地面面積趨於0，長方體的高趨於無窮時，而長方體的體積為1.
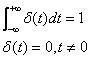二維δ函式 也可叫做衝擊函式。它使用極限語言來定義的一種特殊的函式。δ函式的最常用定義方式為： 形象的說得話就是一個寬度趨近於零而高度趨近於無窮的矩形，其面積為1.
通過上面一維δ函式的定義，我們來延伸到二維空間來。二維δ函式的定義有著與一維相似的定義方式：
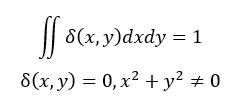二維δ函式 此時形象的說法就是：空間中的一個長方體。當起地面面積趨於0，長方體的高趨於無窮時，而長方體的體積為1.