二元二次型簡介
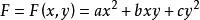 二元二次型
二元二次型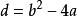 二元二次型
二元二次型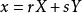 二元二次型
二元二次型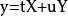 二元二次型
二元二次型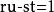 二元二次型
二元二次型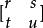 二元二次型
二元二次型二元二次型(binary quadratic form)是二元二次齊次多項式的一種習慣名稱,對固定之整數a,b,c,二次齊次多項式稱為二元二次型或簡稱為型,並以{a,b,c}表示。整數稱為此型之判別式。因此,一個二次型可分解為兩整係數一次式之積的充分必要條件是其判別式為一平方數。若有整係數變換,,將二次型F變為G(X,Y),則稱F與G相似,或稱F經變換而變為G,與正定型相似的二次型亦必為正定型,其中變換矩陣為。
發展沿革
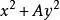 二元二次型
二元二次型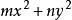 二元二次型
二元二次型二元二次型理論起源於不定方程與整數的加法表示問題。自希臘的Diophantus(246~330)在《算術》中注意到某些特殊的數,特別是平方數之後,把每個正整數都表示成若干特殊的數之和就成了許多數學家追求的目標。法國數學家PierredeFermat(1601~1665)與瑞士數學家Leonard Euler(1707~1783)先後研究了特殊的二元二次型以及。可以說17、18世紀的數論研究,基本上是憑藉數學家的才智和技巧一個一個地解決問題。他們把提出問題和解決問題分割開來,一個問題需要一種特殊的理論和技巧,幾乎有多少問題就有多少理論,這種混亂狀況久而久之便減弱了人們的研究熱情。
18世紀行將結束的時候,數論中那些零碎的散亂局面有了變化。Joseph LoutsLagrange(1736~1813)的二元二次型理論標誌著數論研究方法上的一個飛躍,孕育著一種新的時代精神。他考慮了一般的二元二次型理論。他的探索不是僅僅針對個別的型,而是囊括所有型,是一種高度抽象的理論研究,他從一大堆互不關聯的結果的叢集中走上了統一理論的道路。Lagrange通過其約化理論,對型進行分類,把對“無窮”的研究化簡成對“有限”的研究,從數學思想發展的角度來說,這一點特別有意義。
19世紀Carl Friedrich Gauss(1777~1855)的《算術研究》(Disquisitiones Arithmeticae)的出版,標誌著二元二次型理論的研究進入了一個新的篇章。他在Lagrange的基礎上進一步找到了求各種型的約化型的方法,然後根據約化型把所有型分成有限個等價類,進而開闢了一個全新的領域—型的合成理論。此部分是本文的重點與難點,因為其中涉及到一種重要的數學結構—群。現有的一些文獻曾討論過群的起源問題,Lobos Novy從代數學角度詳細地分析了群的起源,Hanswussing巨觀地從代數、數論、幾何三個方面闡述了群的起源。本文在花費大量精力認真研讀Gauss原著的基礎上,克服重重困難,詳盡地分析了群在數論中二元二次型理論中的起源,以期能向讀者展示出:早在1801年,Gauss的工作就己經孕育著群的思想。此外,二元二次型理論並不是孤立的一部分,它對當今代數數論的產生以及一般二次型的發展都有著重要影響。
二元二次型理論的影響
二元二次型理論開闢了兩大領域。 一是Gauss在研究二元二次型的整數解時,把有理數域和有理整數環上的初等數論問題,放到更大的域和環——二次域和它的(代數)整數環上來研究。他在這方面的工作是研究二次域的開端,也是代數數論的開端。二是除了二次域之外,三次域、四次域乃至一般代數數域與二次型沒有關係,同時多元二次型與代數數論也沒有關係。這樣,二元二次型理論發展成為一般二次型理論。
總之,很長一段時間以來,至少是從Fermat到Minkowski這段時期—二次型理論一直是數論中的一部分。18和19世紀那些偉大的數論學家的大部分著名工作都與二次型的問題有關。在這些工作的基礎上,Minkowski, Siegel、Hasse、Eichler和其他一些人創立了二次型的算術理論,這一理論是Bachrnann、 Eichler和O'Meara著名著作的課題。與此平行發展的是Dedekind、Frohenius、E. Noether和Artin發展起來的抽象代數與抽象線性代數的思想,這些思想導致了現代結構數學,它主要強調分類問題與一般結構定理。
在這二者(二次型的數論和現代代數思想)的基礎之上,1937年Witt開創了二次型理論的一個新篇章。他最富成果的思想是:他不是只考慮“單個”二次型,而是考慮一個固定的基本域上的全體型的實體,從中構造出一種代數對象。這一對象——Witt環後來成為了整個理論的主要對象。三十年後,Pfiter用他著名的結構定理證明了這一方法的重要性。從那時起,這一領域的每個人都清楚地知道存在著一種漂亮的二次型代數數論,人們只需將其揭示出來。

