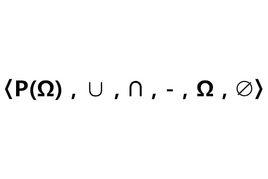基本介紹
事件代數
事件代數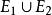
事件代數
事件代數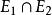
事件代數
事件代數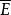 事件代數 事件代數 事件代數 事件代數 事件代數 事件代數 事件代數事件代數是用於合成事件(適當定義的理想試驗的結果)的模型。如果表示這種事件，那么： 表示事件(命題)E或E(或者二者，可兼的或)。 表示事件(命題)E且E。 表示事件(命題)非E。 表示必然事件(所有可能結果的並)。O表示不可能事件 。事件代數亦稱事件場、事件域。理論機率論中的概念，是關於一切有限次的運算封閉的非空事件組。稱事件組為一事件域，如果滿足條件：1. 必然事件Ω∈; 2.若A∈，則其對立事件Ā∈;3.若對於任意n≥2， 事件A， …，A∈，則A∈。任何事件域都含必然事件和不可能事件；若n個事件屬於，則它們經有限次並、交、相減，所得結果仍然是中的事件。
相關說明
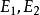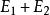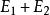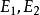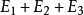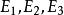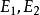事件代數
事件代數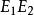 事件代數 事件代數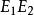
事件代數
事件代數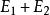 事件代數
事件代數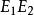 事件代數 事件代數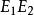 事件代數 事件代數事件代數是由二元布爾代數的另一解釋導出一種可套用於機率論的數學模型，機率論研究的是事件發生的可能性；所謂事件，指的是試驗或觀測的結果。比如投擲一枚骰子是一種試驗，而擲出特定的點數，如4，就是一個事件；因骰子有六個面，所以在這種情況下共有六個可能事件 。在一次給定的試驗中，一個事件可能發生也可能不發生，若令事件的發生、不發生分別對應於二元布爾代數中的1，0，就得到一個一一對應。對於事件定義兩種運算——並(或邏輯加法)與交(或邏輯乘法)，這兩種運算等價於圻取與合取。事件的並記作。於是，若=1，則或是E發生，或是E發生，或是兩者都發生。類似地，若=1，則事件中至少有一個發生，並運算相當於二元布爾代數中的加法。事件的交記作，於是，若=1，則E與E兩者同時發生，交運算相當於二元布爾代數中的乘法。事件E的補(互補事件或對立事件)記作E'，若E=1，則E'=0；若E=0，則E'=1。事件的交與並的運算表與二元布爾代數的運算表完全相同，因此，在交、並運算下事件構成的代數與邏輯乘法、加法運算下的二元布爾代數同構，從而布爾代數的公理、定理對於事件都成立，文氏圖也可用來說明事件的組合，以上這些結論在機率論中都有套用。還要指出包含關係的一個重要結果：=E或=E，都表示E包含於E之中，因此，若且唯若=0時，我們說E與E是互斥的 。
