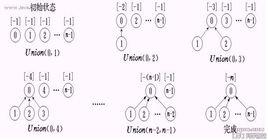
主要操作
初始化
把每個點所在集合初始化為其自身。
通常來說,這個步驟在每次使用該數據結構時只需要執行一次,無論何種實現方式,時間複雜度均為O(N)。
查找
查找元素所在的集合,即根節點。
合併
將兩個元素所在的集合合併為一個集合。
通常來說,合併之前,應先判斷兩個元素是否屬於同一集合,這可用上面的“查找”操作實現。
例題
Description
若某個家族人員過於龐大,要判斷兩個是否是親戚,確實還很不容易,給出某個親戚關係圖,求任意給出的兩個人是否具有親戚關係。 規定:x和y是親戚,y和z是親戚,那么x和z也是親戚。如果x,y是親戚,那么x的親戚都是y的親戚,y的親戚也都是x的親戚。
Input
第一行:三個整數n,m,p,(n< =5000,m< =5000,p< =5000),分別表示有n個人,m個親戚關係,詢問p對親戚關係。 以下m行:每行兩個數Mi,Mj,1< =Mi,Mj< =N,表示Mi和Mj具有親戚關係。 接下來p行:每行兩個數Pi,Pj,詢問Pi和Pj是否具有親戚關係。
Output
P行,每行一個’Yes’或’No’。表示第i個詢問的答案為“具有”或“不具有”親戚關係。
分析問題實質
初步分析覺得本題是一個圖論中判斷兩個點是否在同一個連通子圖中的問題。對於題目中的樣例,以人為點,關係為邊,建立無向圖如下:
圖0-0-1 {請補充圖解}
比如判斷3和4是否為親戚時,我們檢查3和4是否在同一個連通子圖中,結果是在,於是他們是親戚。又如7和10不在同一個連通子圖中,所以他們不是親戚。
用圖的數據結構的最大問題是,我們無法存下多至(M=)2 000 000條邊的圖,後面關於算法時效等諸多問題就免談了。
用圖表示關係過於“奢侈”了。其實本題只是一個對分離集合(並查集)操作的問題。
我們可以給每個人建立一個集合,集合的元素值有他自己,表示最開始時他不知道任何人是它的親戚。以後每次給出一個親戚關係a, b,則a和他的親戚與b和他的親戚就互為親戚了,將a所在集合與b所在集合合併。對於樣例數據的操作全過程如下:
輸入關係 分離集合
初始狀態
(2,4) {2,4}
(5,7) {2,4} {5,7}
(1,3) {1,3} {2,4} {5,7}
(8,9) {1,3} {2,4} {5,7} {8,9}
(1,2) {1,2,3,4} {5,7} {8,9}
(5,6) {1,2,3,4} {5,6,7} {8,9}
(2,3) {1,2,3,4} {5,6,7} {8,9}
最後我們得到3個集合{1,2,3,4}, {5,6,7}, {8,9},於是判斷兩個人是否親戚的問題就變成判斷兩個數是否在同一個集合中的問題。如此一來,需要的數據結構就沒有圖結構那樣龐大了。
算法需要以下幾個子過程:
(1) 開始時,為每個人建立一個集合SUB-Make-Set(x);
(2) 得到一個關係後a,b,合併相應集合SUB-Union(a,b);
(3) 此外我們還需要判斷兩個人是否在同一個集合中,這就涉及到如何標識集合的問題。我們可以在每個集合中選一個代表標識集合,因此我們需要一個子過程給出每個集合的代表元SUB-Find-Set(a)。於是判斷兩個人是否在同一個集合中,即兩個人是否為親戚,等價於判斷SUB-Find-Set(a)=SUB-Find-Set(b)。
有了以上子過程的支持,我們就有如下算法。
PROBLEM-Relations(N, M, a1,…,aM, b1,…,bM, Q, c1,…,cQ, d1,…,dQ)
1 for i←1 to N
2 do SUB-Make-Set(i)
3 for i←1 to M
4 do if SUB-Find-Set(ai) != SUB-Find-Set(bi)
5 then SUB-Union(ai, bi)
6 for i←1 to Q
7 do if SUB-Find-Set(ci)=SUB-Find-Set(di)
8 then output “Yes?”
9 else output “No?”
解決問題的關鍵便為選擇合適的數據結構實現並查集的操作,使算法的實現效率最高。
注意事項
本題的輸入數據量很大,這使得我們的程式會在輸入中花去不少時間。如果你用Pascal寫程式,可以用庫函式SetTextBuf為輸入檔案設定緩衝區,這可以使輸入過程加快不少。如果你是用C語言的話,就不必為此操心了,系統會自動分配緩衝區。
單鍊表實現
一個節點對應一個人,在同一個集合中的節點串成一條鍊表就得到了單鍊表的實現。在集合中我們以單鍊表的第一個節點作為集合的代表元。於是每個節點x(x也是人的編號)應包含這些信息:指向代表元即表首的指針head[x],指向表尾的指針tail[x],下一個節點的指針next[x]。
SUB-Make-Set(x)過程設計如下:
SUB-Make-Set(x)
10 head[x]←x
11 tail[x]←x
12 next[x]←NIL
求代表元的SUB-Find-Set(x)過程設計如下:
SUB-Find-Set(x)
13 return head[x]
前兩個過程比較簡單,SUB-Union(a,b)稍微複雜一點。我們要做的是將b所在鍊表加到a所在鍊表尾,然後b所在鍊表中的所有節點的代表元指針改指a所在鍊表的表首節點,如圖所示。
圖0-0-2
過程的偽代碼如下:
SUB-Union(a,b)
14 next[tail[head[a]]]←head[b]
15 tail[head[a]]←tail[head[b]]
16 p←head[b]
17 while p != NIL
18 do head[p]←head[a]
19 p←next[p]
我們來分析一下算法的時間效率。SUB-Make-Set(x)和SUB-Find-Set(x)都只需要O(1)的時間,而SUB-Union(a,b)的時間效率與b所在鍊表的長度成線性關係。最壞情況下,即有操作序列SUB-Union(N-1,N), SUB-Union(N-2,N-1), …, SUB-Union(1,2)時,整個算法PROBLEM-Relations的時間複雜度為O(N+M+N^2+Q)=O(N^2+M+Q)。
由於算法的時間複雜度中O(M+Q)是必需的,因此我們要讓算法更快,就要考慮如何使減小O(N^2)。
我們想到合併鍊表時,我們可以用一種啟發式的方法:將較短的表合併到較長表上。為此每個節點中還需包含表的長度的信息。這比較容易實現,我們就不寫出偽代碼了。
時間複雜度。
首先我們給出一個固定對象x的代表元指針head[x]被更新次數的上界。由於每次x的代表元指針被更新時,x必然在較小的集合中,因此x的代表元指針被更新一次後,集合至少含2個元素。類似地,下一次更新後,集合至少含4個元素,繼續下去,當x的代表元指針被更新 log k 次後,集合至少含k個元素,而集合最多含n個元素,所以x的代表元指針至多被更新 log n 次。所以M次SUB-Union(a,b)操作的時間複雜度為O(NlogN+M)。算法總的時間複雜度為O(NlogN+M+Q)。
並查集森林
並查集的另一種更快的實現是用有根樹來表示集合:每棵樹表示一個集合,樹中的節點對應一個人。圖示出了一個並查集森林。
圖0-0-3
每個節點x包含這些信息:父節點指針p[x],樹的深度rank[x]。其中rank[x]將用於啟發式合併過程。
於是建立集合過程的時間複雜度依然為O(1)。
SUB-Make-Set(x)
20 p[x]←x
21 rank[x]←0
用森林的數據結構來實現的最大好處就是降低SUB-Union(a,b)過程的時間複雜度。
SUB-Union(a,b)
22 SUB-Link(SUB-Find-Set(a),SUB-Find-Set(b))
SUB-Link(a,b)
23 p[a]←b
合併集合的工作只是將a所在樹的根節點的父節點改為b所在樹的根節點。這個操作只需O(1)的時間。而SUB-Union(a,b)的時間效率決定於SUB-Find-Set(x)的快慢。
SUB-Find-Set(x)
24 if x=p[x]
25 then return x
26 else return SUB-Find-Set(p[x])
這個過程的時效與樹的深度成線性關係,因此其平均時間複雜度為O(logN),但在最壞情況下(樹退化成鍊表),時間複雜度為O(N)。於是PROBLEM-Relations最壞情況的時間複雜度為O(N(M+Q))。有必要對算法進行最佳化。
第一個最佳化是啟發式合併。在最佳化單鍊表時,我們將較短的表鏈到較長的表尾,在這裡我們可以用同樣的方法,將深度較小的樹指到深度較大的樹的根上。這樣可以防止樹的退化,最壞情況不會出現。SUB-Find-Set(x)的時間複雜度為O(log N),PROBLEM-Relations時間複雜度為O(N + logN (M+Q))。SUB-Link(a,b)作相應改動。
SUB-Link(a,b)
27 if rank[a]>rank
28 then p←a
29 else p[a]←b
30 if rank[a]=rank
31 then rank←rank+1
然而算法的耗時主要還是花在SUB-Find-Set(x)上。
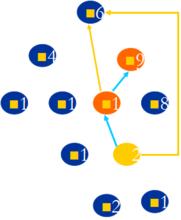
第二個最佳化是路徑壓縮。它非常簡單而有效。如圖所示,在SUB-Find-Set(1)時,我們“順便”將節點1, 2, 3的父節點全改為節點4,以後再調用SUB-Find-Set(1)時就只需O(1)的時間。
圖0-0-4
於是SUB-Find-Set(x)的代碼改為:
SUB-Find-Set(x)
32 if x≠p[x]
33 then p[x]←SUB-Find-Set(p[x])
34 return p[x]
該過程首先找到樹的根,然後將路徑上的所有節點的父節點改為這個根。實現時,遞歸的程式有許多棧的操作,改成非遞歸會更快些。
SUB-Find-Set(x)
35 r←x
36 while r≠p[r]
37 do r←p[r]
38 while x?r
39 do q←p[x]
40 p[x]←r
41 x←q
42 return r
改進後的算法時間複雜度的分析十分複雜,如果完整的寫出來足可寫一節,這裡我們只給出結論:改進後的PROBLEM-Relations其時間複雜度為O(N+(M+Q)*A(M+Q,N)),其中A(M+Q,N)為Ackerman函式的增長極為緩慢的逆函式。你不必了解與Ackerman函式相關的內容,只需知道在任何可想像得到的並查集數據結構的套用中,A(M+Q,N)≤4,因此PROBLEM-Relations的時間複雜度可認為是線性的O(N+M+Q)。
最佳化路徑壓縮
思想
每次查找的時候,如果路徑較長,則修改信息,以便下次查找的時候速度更快。
實現
第一步,找到根結點。
第二步,修改查找路徑上的所有節點,將它們都指向根結點。
代碼
圖示
 並查集
並查集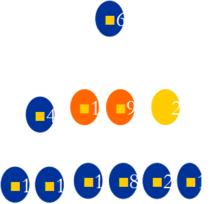 並查集
並查集