基本介紹
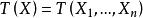 不變統計量
不變統計量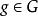 不變統計量
不變統計量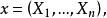 不變統計量
不變統計量不變統計量(invariant statistic)是當對樣本作某種變換時,其值保持不變的統計量。設G= {g}是樣本空間到自身的某種一對一變換的全體(變換群)。稱統計量 關於G為不變統計量,如果對於任意變換 和幾乎一切樣本值 有
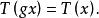 不變統計量
不變統計量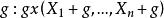 不變統計量
不變統計量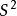 不變統計量
不變統計量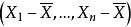 不變統計量
不變統計量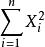 不變統計量
不變統計量其中gx表示由樣本點x經變換g所得新樣本點(即x的象點)。如,對於加以常數g的推移變換 ,樣本方差 是不變統計量。稱關於G的不變統計量為“ 最大不變統計量”,若任何關於G的不變統計量都是該統計量的函式。如,對推移變換, 是最大不變統計量;對於正交變換, 是最大不變統計量 。
不變檢驗
許多統計推斷問題——參數估計和假設檢驗問題——本身呈現出某種不變性,此時要求使用的統計方法也應呈現出相應的不變性。
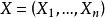 不變統計量
不變統計量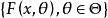 不變統計量
不變統計量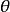 不變統計量
不變統計量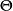 不變統計量
不變統計量設 是從具有分布函式族 中抽取的一個簡單隨機子樣,其中 是未知參數, 是參數空間,即 容許假設。
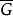 不變統計量
不變統計量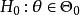 不變統計量
不變統計量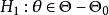 不變統計量
不變統計量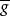 不變統計量
不變統計量 不變統計量
不變統計量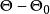 不變統計量
不變統計量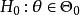 不變統計量
不變統計量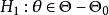 不變統計量
不變統計量設G是一個不變變換群, 是G的導出變換群, 對於原假設 對備選假設 的檢驗問題,如果g的導出變換 ,它既是 自身上的一一對應可逆變換,:也是 自身上的一一對應可逆變換,則稱該檢驗阿題在g變換下保持不變。如果對每個 檢驗問題 對 在g變換下保持不變,則稱該檢驗問題在G 變換下保持不變 。
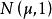 不變統計量
不變統計量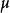 不變統計量
不變統計量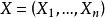 不變統計量
不變統計量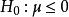 不變統計量
不變統計量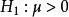 不變統計量
不變統計量例1 設母體服從正態 分布, 是未知參數, 是取自該母體的一子樣,考察檢驗問題:原假設 對備選假設 。
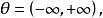 不變統計量
不變統計量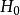 不變統計量
不變統計量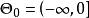 不變統計量
不變統計量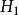 不變統計量
不變統計量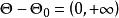 不變統計量
不變統計量此例的容許假設是 原假設 對應的子集是 ,備選假設 所對應的子集是 。
考察尺度變換群
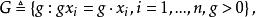 不變統計量
不變統計量它的導出變換群是
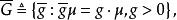 不變統計量
不變統計量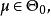 不變統計量
不變統計量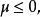 不變統計量
不變統計量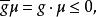 不變統計量
不變統計量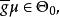 不變統計量
不變統計量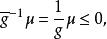 不變統計量
不變統計量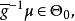 不變統計量
不變統計量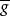 不變統計量
不變統計量 不變統計量
不變統計量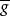 不變統計量
不變統計量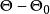 不變統計量
不變統計量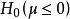 不變統計量
不變統計量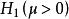 不變統計量
不變統計量對任一 由於g>0,所以如果 即 則 即 和 即 這證明了 是 自身上的一一對應可逆變換,類似地可證明 也是 自身上的一一對應可逆變換,也就是說檢驗問題 對 在g變換下保持不變。由g的任意性得到,該檢驗問題在尺度變換群G之下是不變的。
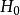 不變統計量
不變統計量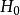 不變統計量
不變統計量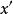 不變統計量
不變統計量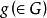 不變統計量
不變統計量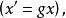 不變統計量
不變統計量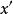 不變統計量
不變統計量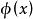 不變統計量
不變統計量因為對於假設檢驗問題,僅採取兩種可能的決策:接受 或拒絕 。因此對於在G變換下保持不變的檢驗問題,不變原理要求如果 是變換 作用到原數據x上所得到的新數據 那末由 所作出的決策應和由x所作出的決策一致。也就是說,檢驗函式 滿足條件
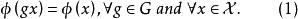 不變統計量
不變統計量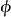 不變統計量
不變統計量(實際上,上式僅要求對幾乎所有的x成立)滿足上式的檢驗 被稱為是關於G不變的;簡稱為 不變檢驗。
如果一個檢驗問題在某個變換群之下是不變的,此時不變原理要求致力於考慮不變檢驗,然後在不變檢驗類中尋找最優檢驗,對於許多檢驗問題,它不存在一致最優勢檢驗,而可以在較小的不變檢驗類中存在一致最優勢不變檢驗。因此不變性與無偏性相類似,它也是一種附加在檢驗法上的比較合理的限制。
為了尋找最優的不變檢驗,先考察不變檢驗的特徵,由(1)式可以看到,在集合
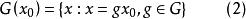 不變統計量
不變統計量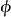 不變統計量
不變統計量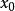 不變統計量
不變統計量上, 必保持常數。習慣上稱由(2)式所定義的集合 為 關於G 的跡。
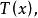 不變統計量
不變統計量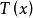 不變統計量
不變統計量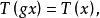 不變統計量
不變統計量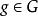 不變統計量
不變統計量 不變統計量
不變統計量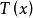 不變統計量
不變統計量如果一個纜計量 它在每個跡上保持常數,也就是說, 演足關係式 對一切 和幾乎所有的 ,則稱 是關於G 的 不變統計量,顯然不變檢驗一定是不變統計量。
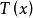 不變統計量
不變統計量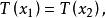 不變統計量
不變統計量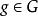 不變統計量
不變統計量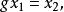 不變統計量
不變統計量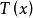 不變統計量
不變統計量若一個不變統計量 ,如果有 則存在 ,使得 這樣的 稱為 最大不變統計量。直觀地說最大不變統計量在每個跡上保持常數,且在不同的跡上取不同的常數 。
相關定理
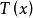 不變統計量
不變統計量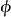 不變統計量
不變統計量定理1 設 是關於G的最大不變統計量,則檢驗函式 是不變檢驗的充要條件是存在函式h,使得
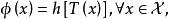 不變統計量
不變統計量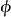 不變統計量
不變統計量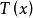 不變統計量
不變統計量 不變統計量
不變統計量也就是說 僅通過 依賴於 。
證明: 如果
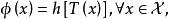 不變統計量
不變統計量則
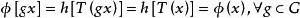 不變統計量
不變統計量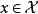 不變統計量
不變統計量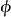 不變統計量
不變統計量和 ,所以 是不變檢驗。
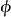 不變統計量
不變統計量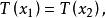 不變統計量
不變統計量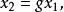 不變統計量
不變統計量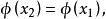 不變統計量
不變統計量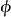 不變統計量
不變統計量反之,如果 是不變的,且 則由於T是最大不變的,因此一定存在g使得 所以 即 通過T依賴於x。
定理1的結論實際上對一切不變統計量都成立。
定理1指出,任何一一個不變檢驗都是最大不變統計量的函式,但是最大不變統計量仍很複雜,因此此時基於最大不變統計量尋找最優不變檢驗仍是困難的。最優檢驗可以在由充分統計所構造的檢驗類里去尋找。因此如果我們能夠找到關於最大不變統計量的導出分布族的充分統計量,即最大不變充分統計量。那么最優不變檢驗就可以局限在由最大不變充分統計量所構造的檢驗類里去尋找。
如何尋找最大不變充分統計量呢? 按照常規的路徑是先尋找最大不變統計量,及由最大不變統計的導出分布族,然後求出關於該導出分布族的充分統計,按此路徑求最大不變充分統計量是困難的。Stein指出,在一定的條件下,最大不變充分統計量是關於充分統計的最大不變統計量,也就是說,此時我們可以先找出充分統計,然後對充分統計考察它在G 變換下的最大不變統計,通過這一路徑尋找最大不變充分統計量往往比較方便 。

