定義
矩陣中每個主對角元素的模都大於與它同行的其他元素的模的總和.這種矩陣就叫‘嚴格對角占優的’;對列同樣成立
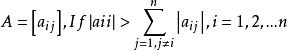 對角占優矩陣
對角占優矩陣(1)設 ,則稱A為嚴格對角占優矩陣。
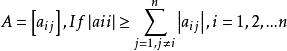 對角占優矩陣
對角占優矩陣(2)設 且其中至少有一個式子取嚴格不等號,則稱A為弱對角占優矩陣。
1、若A是嚴格對角占優矩陣,則關於它的線性代數方程組有解。
2、如果A為嚴格對角占優矩陣,則A為非奇異矩陣。
3、若A為嚴格對角占優矩陣,則雅克比疊代法、高斯-賽德爾疊代法和0<ω≤1的超鬆弛疊代法均收斂。
對角占優矩陣的塊判定
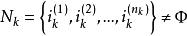 對角占優矩陣
對角占優矩陣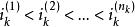 對角占優矩陣
對角占優矩陣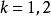 對角占優矩陣
對角占優矩陣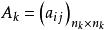 對角占優矩陣
對角占優矩陣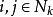 對角占優矩陣
對角占優矩陣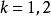 對角占優矩陣
對角占優矩陣記 , , , , , 。
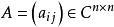 對角占優矩陣
對角占優矩陣 對角占優矩陣
對角占優矩陣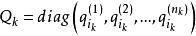 對角占優矩陣
對角占優矩陣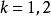 對角占優矩陣
對角占優矩陣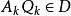 對角占優矩陣
對角占優矩陣定理1:設 ,則 為廣義嚴格對角占優矩陣的充要條件是存在兩個正對角矩陣 , ,使 ,且2階非復矩陣
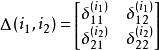 對角占優矩陣
對角占優矩陣為廣義對角占優矩陣。
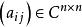 對角占優矩陣
對角占優矩陣 對角占優矩陣
對角占優矩陣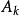 對角占優矩陣
對角占優矩陣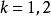 對角占優矩陣
對角占優矩陣定理2:設 為不可約矩陣,則 為廣義嚴格對角占優矩陣的充要條件是 為廣義嚴格對角占優矩陣( )。
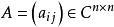 對角占優矩陣
對角占優矩陣 對角占優矩陣
對角占優矩陣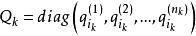 對角占優矩陣
對角占優矩陣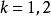 對角占優矩陣
對角占優矩陣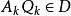 對角占優矩陣
對角占優矩陣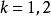 對角占優矩陣
對角占優矩陣定理3:設 為不可約矩陣,則 為廣義嚴格對角占優矩陣的充要條件是存在兩個正對角矩陣 , ,使 , ,2階非負矩陣
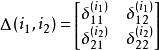 對角占優矩陣
對角占優矩陣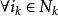 對角占優矩陣
對角占優矩陣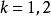 對角占優矩陣
對角占優矩陣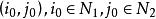 對角占優矩陣
對角占優矩陣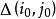 對角占優矩陣
對角占優矩陣為嚴格對角占優矩陣,,且至少存在一對使為廣義嚴格對角占優矩陣。

