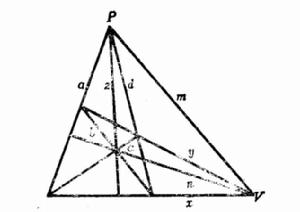
基本概念
平面上所有點的集合稱為點場,該平面稱為點場的底抄。平面上所有直線的集合稱為線場, 該平面稱為線場的底自。其實,點場互、線場在某種意義下都是平面的同義語,二維基本圖形是點場與線場的統稱動。
除了以上基本的平面形以外,還有許多平面形,不勝枚舉。舉例如下:
三點形——三個不共線的點以及其中每兩點連結而成的三條直線的集合,稱為三點形,這三個點稱為三點形的頂點,連結它們的直線稱為三點形的邊。
三線形——三條不共點的直線以及其中每兩條直線的三個交點的集合,稱為三線形 。
平面射影幾何的對偶原理
點與直線是射影平面上的基本元素,平面射影幾何主要研究點與直線以及它們的相互關係,統稱為結合關係。在一個僅涉及點與直線以及它們的結合關係的命題中,把點改成直線,直線改成點,結合關係也作相應的改變。例如,兩點連線中點改成直線,直線改成點得到:兩直線交點;又例如,三點共線改成三直線共點,這樣改變以後得到一個新的射影幾何命題,稱為原命題的對偶命題,下面是一些互為對偶的命題 :
(1)兩點決定一直線,即過兩不同點有且只有一條直線。
(1)'兩直線有且只有一個交點。
(2)由不共線的三點及它們的兩兩連線構成的圖形叫三點形。
(2)'由不交於一點的三直線及它們的兩兩交點構成的圖形叫三線形。
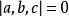 三線形
三線形 (3)射影坐標下,三點A,B,C共線的充要條件是 。
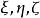 三線形
三線形 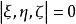 三線形
三線形 (3)'射影坐標下,三直線 共點的充要條件是 。
(4)如果兩個三點形的對應頂點連線交於一點,則它們的對應邊交點共線。
(4)'如果兩個三線形的對應邊交點共線,則它們的對應頂點連線共點。
(5)四點中總有三點共線(不成立)。
(5)'四直線中總有三直線共點(不成立)。
從上面可以看出,如果一個射影幾何的關於點,直線以及它們的結合關係的命題是真實的,它的對偶命題也是真實的,對偶命題是相互的,即如果命題B是A的對偶命題,那么A也是B的對偶命題。上述對偶命題中(4)是Desargues定理,而(4)'實際上是它的逆定理。
在射影幾何的對偶中,點與直線是最基本的對偶元素,“點在直線上”與“直線過點”是最基本的對偶關係。
對偶原理 在平面射影幾何里,如果一個關於點和直線的結合關係的命題成立,則它的對偶命題也成立。
射影幾何可以用公理法來定義並討論,對偶原理也可用公理法證明。一種射影映射——對射,它把點變成直線,直線變成點,而點與直線的結合關係仍能保持,利用對射可以證明對偶原理,在射影坐標下,計算兩點連線與兩直線交點的方法、判斷三點共線與三線共點的方法都是一樣的,只要把點與直線的坐標互換 。