三段論公理

凡對全類有所肯定，則對全類的分子也有所肯定； 凡對全類有所否定，則對全類的分子也有所否定。 圖2表示：s類包含於m類，m類與p類全異，所以，s類與p類全異。

就是在一切關於三段論的規則推導的討論之前必須先行接受的東西，而且它被約定不證自明，為理性所普遍接受，三段論其他規則都由他衍生出來。
三段論公理在嚴復譯J.S.Mill的《穆勒名學》中，它被譯作“曲全公例”，可表述如下：
凡對全類有所肯定，則對全類的分子也有所肯定；
凡對全類有所否定，則對全類的分子也有所否定。
三段論推理的根據：一類事物的全部是什麼或不是什麼，那么這類事物的部分或分子也是什麼或不是什麼，即如果對一類事物的全部有所肯定或否定，那么對它的部分或分子也有所肯定或否定。

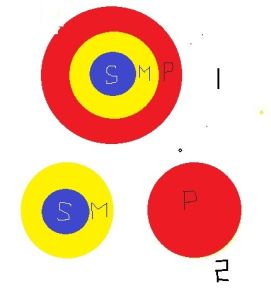圖

從概念的外延方面看，
圖1表示：s類包含於m類，m類包含於p類，所以，s類包含於p類；
圖2表示：s類包含於m類，m類與p類全異，所以，s類與p類全異。
三段論公理的客觀基礎就是類與類的包含關係和全異關係，是人類億萬次重複實踐中總結出來的不證自明的性質。我們數學證明的目的----就是獲得一類事物（數學概念）的性質，三段論公理是我們在證明一個定理過程中幾個板塊對接的基本要求。