簡介
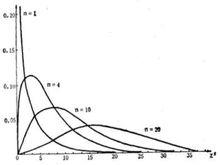三大抽樣分布如圖
χ2分布
定義
設 X,X,......X相互獨立, 都服從標準常態分配N(0,1), 則稱隨機變數χ =X +X +......+X 所服從的分布為自由度為 n 的χ2分布.
結論
期望E（χ ）=n，方差D(χ )=2n。
χ2分布具有可加性。若χ ~χ (n),χ ~χ (m)，且二者相互獨立，則χ +χ ~χ (n+m)。
t分布
定義
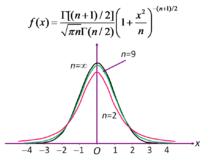t分布設X1服從標準常態分配N(0,1)，X2服從自由度為n的χ2分布，且X1、X2相互獨立，則稱變數t=X1/（X2/n） 所服從的分布為自由度為n的t分布。
結論
期望 E（T）=0，方差 D(T)=n/(n-2),n>2
F分布
定義
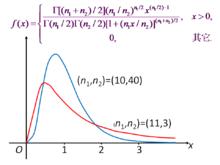F分布設X1服從自由度為m的χ2分布,X2服從自由度為n的χ2分布，且X1、X2相互獨立，則稱變數F=(X1/m)/(X2/n)所服從的分布為F分布，其中第一自由度為m,第二自由度為n.
結論
1.期望E(F)=n/(n-2)，方差D(F)=2n^2(m+n-2)/m(n-2)^2(n-4)
2.若F~F(m,n)，則1/F~F(n,m)
3.若F~F(1,n)，T~T(n)，則F=T^2
