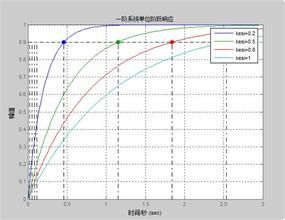
簡介
英文名稱： first-order system.
定義：凡是可用一階微分方程描述的系統稱一階系統。從零極點角度來講，系統函式最多只含有一個極點和一個零點的系統是一階系統。在一階系統中，一般只含有一個儲能元件，或者是電容，或者是電感。
微分方程：τdy(t)/dt+y(t)=s0x(t)，其中τ–系統時間函式；s0–系統靈敏度。
傳遞函式：H(s)=s0/(τs+1)
頻率回響函式：H(ω)=s0/(jτω+1)
相關簡介
一個系統階數是由此系統包含多少狀態變數決定的。
一個複雜的高階的系統從結構上可分解成若干的低階子系統。
複雜系統的特性並不等於組成它的簡單子系統的特性之和。
一個複雜系統的行為往往是由某些主迴路和某些主要的變數決定的
複雜系統中往往存在一些起主導作用的主迴路或主要變數。
一階系統的重要參數
指數增長及其參數
（1）指數增長方程式
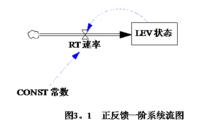一階系統LLEV.K=LEV.J+DT*（RT.JK）
由此式可以改寫為：
（LEV.K-LEV.J）/DT=RT.JK
脫去DYNAMO的符號，並令DT趨於0，則可得微分方程式：
dLEV(t)/dt=RT(t)
假定
RT(t)=CONST*LEV(t)CONST為比例常數
所以
dLEV(t)/dt=CONST*LEV(t)
可解的：
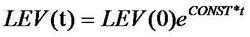一階系統式中：
LEV(t)——狀態在t時刻的值；
LEV(0)——狀態的初始值；
CONST——比例常數；
e——自然對數基。
（2）時間常數T
時間常數定義為CONST的倒數，即T=1/CONST，T具有時間的量綱。
P91時間常數的物理意義。
時間常數T決定正反饋系統中的增長或減少的速度。當時間常數大時（或CONST小），相應的LEV（t）為較平緩的增長曲線。反之，LEV（t）為較陡峭的變化曲線。
（3）倍增時間Td
倍增時間定義為變數由初始值增至二倍的初始值所需要的時間。
Td=0.69*T
倍增時間約等於70%的時間常數T。即每經過一段時間Td，LEV的值將較前增加一倍。
一階負反饋系統的重要參數
方程式的基本形式
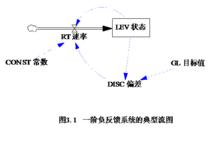一階系統方程式：
LLEV.K=LEV.J+DT*RT.JK
RRT.KL=CONST*DISC.K
ADISC.K=GL-LEV.K
同理解得：
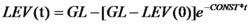一階系統減半時間常數（或半衰期）Th
Th=0.69T
