公式
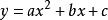二次函式一般式二次函式一般式
已知三點求二次函式解析式（]]y=ax^2b]i]]]+bx+cb]i])
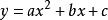二次函式一般式可設二次函式解析式為：
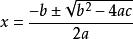二次函式一般式二次公式為：
求解方法
知道3點了，分別代入這個解析式，就可以得出3個方程，3個方程，3個未知數，就可以求出a，b，c了。
其他求法
如果3個交點中有2個交點是二次函式與x軸的交點。
那么，可設這個二次函式解析式為：y=a（x-x1）（x-x2）（x1，x2是二次函式與x軸的2個交點坐標），根據另一個點就可以求出二次函式解析式。
如果知道頂點坐標為（h，k），則可設：y=a（x-h）²+k，根據另一點可求出二次函式解析式。
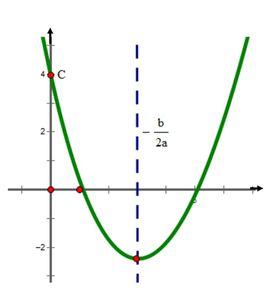
圖像關係
a、b、c值與圖像關係
a>0時，拋物線開口向上；a<0時，拋物線開口向下。
當拋物線對稱軸在y軸左側時a,b同號，當拋物線對稱軸在y軸右側時a,b異號。
c>0時，拋物線與y軸交點在x軸上方；c<0時，拋物線與y軸交點在x軸下方。
a=0時，此圖像為一次函式。
b=0時，拋物線頂點在y軸上。
c=0時，拋物線在x軸上。
當拋物線對稱軸在y軸左側時a,b同號，當拋物線對稱軸在y軸右側時a,b異號。
