定義
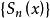 一致收斂性
一致收斂性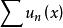 一致收斂性
一致收斂性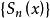 一致收斂性
一致收斂性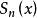 一致收斂性
一致收斂性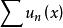 一致收斂性
一致收斂性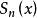 一致收斂性
一致收斂性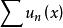 一致收斂性
一致收斂性函式項級數的一致收斂性:設 是函式項級數 的部分和函式列,若 在數集D上一致收斂於函式 ,則稱函式項級數 在D上一致收斂於函式 ,或稱函式項級數 在D上一致收斂。
判別方法
函式項級數作為數項級數的推廣,一致收斂性的判別法類似於數項級數,都有Cauchy判別法、Abel判別法、Dirichlete判別法等。另外,結合數項級數的比式判別法和根式判別法,可以得到函式項級數一致收斂性的比式判別法和根式判別法,同時利用p 級數的收斂性和優級數判別法還可得到函式項級數一致收斂性的對數判別法 。
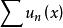 一致收斂性
一致收斂性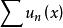 一致收斂性
一致收斂性在這些方法中,柯西準則判別法和魏爾斯特拉斯判別法是較為實用和方便的一致收斂判別法,一般要首先考慮使用。如果能用魏爾斯特拉斯判別法判定 一致收斂,則 必定是絕對收斂,從而魏爾斯特拉斯判別法對條件收斂的函式項級數失效。
定義判別法
根據定義判別函式列是否一致收斂。
柯西準則判別法
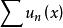 一致收斂性
一致收斂性函式項級數 在D上一致收斂的充分必要條件是對於任意給定的ε>0,存在正整數N=N(ε),使
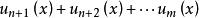 一致收斂性
一致收斂性| |<ε對一切正整數m>n>N與一切x∈D成立。
阿貝爾判別法
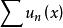 一致收斂性
一致收斂性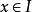 一致收斂性
一致收斂性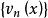 一致收斂性
一致收斂性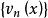 一致收斂性
一致收斂性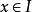 一致收斂性
一致收斂性設(Ⅰ)
在區間I上一致收斂;(Ⅱ)對於每一個,是單調的;
(Ⅲ)在I上一致有界,即對一切和正整數n,存在正整數M,使得
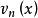 一致收斂性
一致收斂性| |<=M,
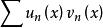 一致收斂性
一致收斂性則級數 在I上一致收斂。
狄利克雷判別法
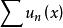 一致收斂性
一致收斂性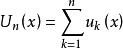 一致收斂性
一致收斂性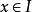 一致收斂性
一致收斂性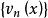 一致收斂性
一致收斂性設 (Ⅰ)
的部分和函式列(n=1,2,3,…)在I上一致有界;(Ⅱ)對於每一個,是單調的;
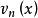 一致收斂性
一致收斂性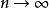 一致收斂性
一致收斂性(Ⅲ)在I上 一致收斂於0( ),
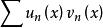 一致收斂性
一致收斂性則 級數 在I上一致收斂。
魏爾斯特拉斯判別法
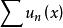 一致收斂性
一致收斂性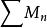 一致收斂性
一致收斂性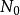 一致收斂性
一致收斂性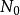 一致收斂性
一致收斂性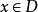 一致收斂性
一致收斂性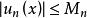 一致收斂性
一致收斂性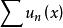 一致收斂性
一致收斂性設 為一個函式項級數,若存在一個收斂的正項級數 ,且存在 ,當n> , 時,有 ,則函式項級數 一致收斂。
比式判別法
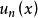 一致收斂性
一致收斂性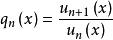 一致收斂性
一致收斂性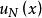 一致收斂性
一致收斂性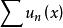 一致收斂性
一致收斂性設 為定義在數集D 上正的函式列,記 ,存在正整數N 及實數q、M, 使得:qn(x)≤ q < 1, ≤M 對任意的n > N ,x ∈ D 成立, 則函式項級數 在D 上一致收斂。
根式判別法
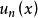 一致收斂性
一致收斂性設 為定義在數集D 上的函式列,若存在正整數N,使得
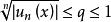 一致收斂性
一致收斂性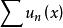 一致收斂性
一致收斂性對所有 n > N,x ∈ D 成立,則函式項級數 在D上一致收斂。
對數判別法
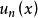 一致收斂性
一致收斂性設 為定義在數集D 上正的函式列,若
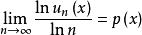 一致收斂性
一致收斂性存在,那么:
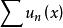 一致收斂性
一致收斂性(1)若對 x ∈ D , p(x) > p > 1, 則函式項級數 在D 上一致收斂;
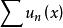 一致收斂性
一致收斂性(2)若對 x ∈ D , p(x) < p < 1, 則函式項級數 在D 上不一致收斂。
性質
一致收斂數列具有連續性、可積性、可微性的性質 。
連續性
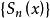 一致收斂性
一致收斂性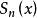 一致收斂性
一致收斂性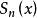 一致收斂性
一致收斂性若函式列 的每一項 均在[ a, b] 上連續,且一致收斂於 , 則其極限函式S(x)也在[ a, b] 上連續。
可積性
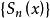 一致收斂性
一致收斂性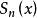 一致收斂性
一致收斂性設 在[ a, b] 上一致收斂於S(x), 每一個 都在[ a, b] 上連續, 那么
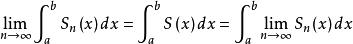 一致收斂性
一致收斂性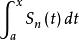 一致收斂性
一致收斂性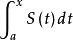 一致收斂性
一致收斂性且函式列 在[ a, b] 上一致收斂於 。
可微性
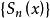 一致收斂性
一致收斂性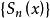 一致收斂性
一致收斂性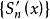 一致收斂性
一致收斂性若在[ a, b] 上,函式列 的每一項都有連續導數, 收斂於S(x), 一致收斂於σ(x), 則S′(x)=σ(x),即
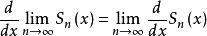 一致收斂性
一致收斂性一致收斂性與非一致收斂性
根據函式項級數的一致收斂性定義和定理,函式項級數的一致收斂性與非一致收斂性的區別:
 一致收斂性
一致收斂性推廣
含參變數廣義積分的一致收斂性:
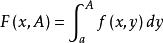 一致收斂性
一致收斂性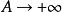 一致收斂性
一致收斂性 一致收斂性
一致收斂性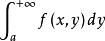 一致收斂性
一致收斂性 一致收斂性
一致收斂性若 ,當 時,對 一致收斂,則稱對一致收斂。

