簡介
一次同餘方程亦稱線性同餘方程,是一類簡單的同餘方程,指未知數僅出現一次冪的同餘方程。
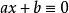 一次同餘方程
一次同餘方程 一次同餘方程
一次同餘方程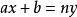 一次同餘方程
一次同餘方程 一次同餘方程
一次同餘方程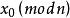 一次同餘方程
一次同餘方程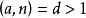 一次同餘方程
一次同餘方程 一次同餘方程
一次同餘方程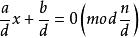 一次同餘方程
一次同餘方程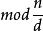 一次同餘方程
一次同餘方程 一次同餘方程
一次同餘方程最簡單的一次同餘方為 (mod n),此處整數 (mod n)及 b 為給定整數,求解 x。這相當於求解一次不定方程(indefinite equation)或一次丟番圖方程(Diophantine equation) ,其中,a,b,n為已知整數,求整數解x,y。這一方程有解的充要條件為(a,n)|b。當 時,同餘方程有唯一的解 。當 時,只有當d|b時有解,這時命 為 唯一的解, 。則原方程共有 d 個關於模 n 互不同餘的解: 。
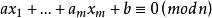 一次同餘方程
一次同餘方程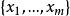 一次同餘方程
一次同餘方程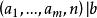 一次同餘方程
一次同餘方程 一次同餘方程
一次同餘方程一般的一次同餘方程 有解 的充要條件為 。若此條件成立,則共有 組互不同餘的解,mod n。
關於一次不定方程,中國古代早有研究,如張丘建的“百雞問”等。
解法
關於一次同餘方程的解法和性質有下述定理:
1.設(a, m) = 1,m>0,則同餘式ax≡b(mod m)恰有一個解;
2.設(a, m) = d,m>0,則同餘式ax≡b(mod m)有解的充分必要條件是d|b,此時恰有d個解。
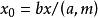 一次同餘方程
一次同餘方程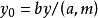 一次同餘方程
一次同餘方程 一次同餘方程
一次同餘方程 一次同餘方程
一次同餘方程根據以上兩個定理,同餘方程ax≡b (mod m)在a≢0且(a,m)|b的條件下,必有(a,m)個關於模m互不同餘的解。又根據最大公約數的性質,必有二整數x、y,能使ax+my=(a,m)。由於(a,m)|b,所以有 , ,使 ,由此即可得到原方程的(a,m)個關於模m互不同餘的解為。

