簡介
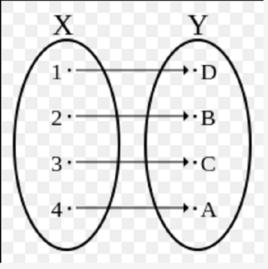
在數學中,雙射,雙射函式或一對一對應是兩組的元素之間的函式,其中一組的每個元素與另一組的元素恰好配對,另一組的每個元素與第一組的正好一個元素也恰好配對。沒有不配對的元素。在數學術語中,雙射函式f:X→Y是集合X與集合Y的一一映射,也叫一一對應。
具體定義
對於X和Y之間的配對(其中Y不需要與X不同)稱為對應,以下四個屬性必須成立:
(1)X的每個元素必須與Y的至少一個元素配對;
(2)沒有X的元素可以與Y的多於一個元素配對;
(3)Y的每個元素必須與X的至少一個元素配對;
(4)Y的任何元素都不能與X的多個元素配對。
滿足屬性(1)和(2)意味著對應是域X的函式。更常見的是將屬性(1)和(2)寫為單個語句:X的每個元素與正好一個元素配對滿足屬性(3)的函式被稱為“到Y”,稱為拋射(或投射函式)。滿足屬性(4)的函式被稱為“一對一函式”,稱為或注入函式。使用這個術語,對應是一種既可以是一種輸出,也可以是一種注入的功能,或者使用其他單詞,對應是“一對一”和“上”的功能。
舉例
打棒球或板球隊的陣容
考慮棒球或板球隊的擊球陣容(或任何運動隊的所有球員的列表,每個球員在陣容中持有特定的位置)。 組X將是球隊中的球員(在棒球的情況下大小為九),組Y將是擊球順序(1st,2nd,3rd等)的位置。由此給出“配對” 玩家在這個順序是在什麼位置。 由於每個玩家都在列表中的某個地方,所以屬性(1)是滿足的。 屬性(2)是滿足的,因為沒有玩家在命中的兩個(或更多)位置。屬性(3)表示,對於每個職位,有一些球員在這個位置擊球,而屬性(4)則指出,兩名或兩名以上的選手不會在列表中同一位置擊球。
座位和學生的教室
在教室里有一定數量的座位。 一群學生進入房間,老師要求他們坐下。 在房間周圍快速瀏覽之後,老師聲明,一組學生和一組座位之間存在雙向偏差,每個學生與他們所在的座位配對。老師為了達成這個結論而觀察到了什麼是:
(1)每個學生都坐在座位上(沒有人站立);
(2)沒有學生在一個以上的座位上;
(3)每個座位都有人坐在那裡(沒有空座);
(4)沒有座位上有不止一名學生。
教練得出的結論是,與學生一樣多的座位,而不必計算任何一套。
逆
具有域X(以功能符號表示的f:X→Y)的雙射f也定義了從Y開始並轉到X(通過轉動箭頭)的關係。對於任意函式“轉動箭頭”的過程通常不產生函式,但是對應的屬性(3)和(4)表示該反向關係是域Y的函式。此外,屬性(1)和(2)然後說這個反函式是一個輸出,一個注入,即反函式存在,也是一個雙射。具有反函式的函式據說是可逆的。若且唯若它是雙向的時候,函式是可逆的。
以簡明的數學符號表示,若且唯若滿足條件時,函式f:X→Y是對應
對於Y中的每個y,在x中存在唯一的x,其中y = f(x)。
繼續使用棒球擊球陣容示例,正在定義的功能以輸入方式輸入玩家之一,並以擊球順序輸出該玩家的位置。由於這個功能是一個雙射,它具有一個反向功能,它將擊球順序中的位置作為輸入,並輸出將在該位置擊球的玩家。
基數
如果X和Y是有限集合,那么若且唯若X和Y具有相同數量的元素時,兩個集合X和Y之間存在對應。 實際上,在公理集理論中,這被認為是“相同數量的元素”(均等)的定義,並將這個定義推廣到無限集,導致基數的概念,一種區分無限集的各種大小的方法。
泛化為部分功能
一一對應的概念概括為部分功能,即將其稱為部分雙射。這種原因是(適當的)部分功能對於其一部分域已經是未定義的;因此沒有強制性的理由將其逆向約束為總功能,即在其域上的任何地方都被定義。給定基集合上的所有部分雙射的集合稱為對稱反半群。
定義相同概念的另一種方式是說,從A到B的部分對應是任何關係R(其證明是部分功能),其特徵在於R是對應f的圖:A'→B' ,其中A'是A的子集,B'是B的子集。
當部分對應處於同一組時,有時稱為一對一部分變換。一個例子是簡單地在複雜平面上定義的莫比斯變換,而不是完成擴展的複雜平面。