wb[磁通量]

簡介

設在磁感應強度為 B的勻強磁場中，有一個面積為 S且與磁場方向垂直的平面，磁感應強度 B與面積 S的乘積，叫做穿過這個平面的磁通量，簡稱磁通（Magnetic Flux）。標量，符號“Φ”。

在一般情況下，磁通量是通過磁場在曲面面積上的積分定義的。其中，Φ為磁通量， B為磁感應強度， S為曲面， B·d S為點積，d S為無窮小矢量（見曲面積分）。磁通量通常通過通量計進行測量。通量計包括測量線圈以及估計測量線圈上電壓變化的電路，從而計算磁通量。

定義

表示磁場分布情況的物理量。通過磁場中某處的面元dS的磁通量dΦ定義為該處磁感應強度的大小B與dS在垂直於B方向的投影dScosθ的乘積，即dFB =BdScosθ式中θ是面元的法線方向n與磁感應強度B的夾角。磁通量是標量，θ<90°為正值，θ>90°為負值。通過任意閉合曲面的磁通量 ΦB 等於通過構成它的那些面元的磁通量的代數和，即對於閉合曲面，通常取它的外法線矢量（指向外部空間）為正。

在一般情況下，磁通量是通過磁場在曲面面積上的積分定義的。

其中，Φ為磁通量， B為磁感應強度， S為曲面， B·d S為點積，d S為無窮小矢量（見曲面積分）。

磁通量通常通過通量計進行測量。通量計包括測量線圈以及估計測量線圈上電壓變化的電路，從而計算磁通量。

公式

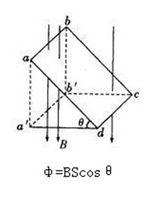在磁場與平面不垂直的情況下磁通量計算公式

Φ=BS，適用條件是B與S平面垂直。如圖，當S與B的垂面存在夾角θ時，Φ=B·S·cosθ。

單位

wb[磁通量]

在國際單位制中，磁通量的單位是韋伯，是以德國物理學家威廉·韋伯的名字命名的。Weber，符號是Wb，1Wb=1T*m =1V*S，是標量，但有正負，正負僅代表穿向。

韋伯可以用法拉第電磁感應定律來推導。1韋伯=10 （1億）麥克斯韋。

性質

通過某一平面的磁通量的大小，可以用通過這個平面的磁感線的條數的多少來形象地說明。在同一磁場中，磁感應強度越大的地方，磁感線越密。因此，B越大，S越大，磁通量就越大，意味著穿過這個面的磁感線條數越多。過一個平面若有方向相反的兩個磁通量，這時的合磁通為相反方向磁通量的代數和（即相反合磁通抵消以後剩餘的磁通量）。

磁場的高斯定理指出，通過任意閉合曲面的磁通量為零，即它表明磁場是無源的，不存在發出或會聚磁力線的源頭或尾閭，亦即不存在孤立的磁單極。以上公式中的B既可以是電流產生的磁場，也可以是變化電場產生的磁場，或兩者之和。

磁通密度是通過垂直於磁場方向的單位面積的磁通量，它等於該處磁場磁感應強度的大小B。磁通密度精確地描述了磁力線的疏密。

通量概念是描述矢量場性質的必要手段，通量密度則描述矢量場的強弱。磁通量和磁通密度，電通量和電通密度都是如此。

磁通量表格

通電導體與磁場方向垂直時，它受力的大小既與導線長度L成正比，又與導線中的電流I成正比，即與I和L的乘積IL成正比，公式是F=ILB，式中B是磁感應強度。

磁通量的定義為覆蓋某面積的磁場的積分

其中Φ為磁通量, B為磁感應強度, S為面積。 已知高斯磁場定律為：Φ= BS。

這條方程的體積積分，跟散度定理合用，給出以下的結果：

亦即是說，通過任何密閉表面的磁通量一定為零；自由“磁電荷”是不存在的。

對比下, 另一條麥克斯韋方程──高斯電場定律為：∫∫E.ds=Q/ε0

電動機原理圖解

其中 E為電場強度， ρ為自由電荷的密度（不包括在物料中被束縛的雙極電荷）， ε0為真空介電常數。 注意這指出了電單極的存在，也就是，自由的正或負電荷。

磁通量密度向量的方向定義為從磁南極到磁北極（磁鐵裡面）。在磁鐵外，場線會由北到南。

若磁場通過能導電的電線環，而磁通量的改變的話，會引起電動勢的生成, 並因此會產生電流（在環中）。其關係式可由法拉第定律得出：

這就是發電機發電的原理。