由BCS理論(見超導微觀理論)知道,庫珀對是長程有序的,因此在一塊超導體中所有的庫珀對具有相同的位相。如果圖2所示的兩塊超導體中間的絕緣層較厚,則兩塊超導體中電子無關聯,各自具有獨立的位相嗞1和嗞2。當絕緣層減小到某一厚度後,兩塊超導體中的超導電子就以位相差嗞=嗞1-嗞2聯繫起來。這時的絕緣層就成為一個“弱”超導體。庫珀對可通過這個“弱”超導體而出現超流隧道或電子對隧道效應。約瑟夫森從理論上得到超導隧道電流密度Js與位相差的關係為
公式
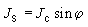 磁通量穿透深度
磁通量穿透深度式中Jc與兩塊超導體的性質和絕緣層的厚度以及所處的溫度有關。
約瑟夫森同時指出,位相嗞受電壓V或磁場H)的調製,嗞與V或H)的關係為
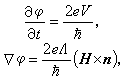 磁通量穿透深度
磁通量穿透深度式中約瑟夫森穿透深度和d分別為超導體1和2的磁場穿透深度,d為絕緣層厚度,r為垂直於結平面的單位矢量。
如果只在結兩端加恆電壓V,則
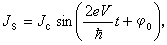 磁通量穿透深度
磁通量穿透深度這就是交流約瑟夫森效應。
如果只加一平行於結面的磁場,則
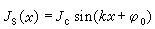 磁通量穿透深度
磁通量穿透深度式中對結面積積分就可以得到結的總電流
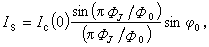 磁通量穿透深度
磁通量穿透深度式中;是穿透到約瑟夫森結中的磁通量,是磁通量子。Is的最大值為
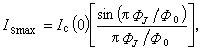 磁通量穿透深度
磁通量穿透深度
