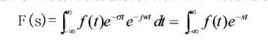簡介
這種分析方法在信號分析和處理等領域占有重要地位。不過這種方法也有局限性,譬如雖然大多數實際信號都存在傅立葉變換,但也有些重要信號不存在傅立葉變換,如按指數增長的信號。
在這種情況下引入s=σ+jω(σ、ω均為實數),以復指數exp(st)為基本信號,任意信號可分解為眾多不同復頻率的復指數分量,而LTI系統的零狀態回響是輸入信號個分量所引起回響的積分(拉普拉斯變換),而且若考慮到系統的初始狀態則系統的零輸入回響也可以同時求得,從而得到系統的全回響。
發展
19世紀末,英國工程師赫維賽德發明了“運算法”,為電工程計算遇到的一些基本問題提供了廣闊通途。他所進行的工作成為拉普拉斯變換法的先驅,該方法很快被許多人採用,但是由於當時缺少嚴密的數學論證,因此,曾受到某些數學家的譴責。然而,赫維賽德及另一些追隨他的學者堅信這一方法的正確性,他們繼續堅持不懈的深入研究,後來人們終於在法國數學家拉普拉斯的著作中為赫維賽德運算法找到了可靠的數學依據並重新給予了嚴密的數學定義,最終為之取名為拉普拉斯變換。
從此,拉氏變換法在電學、力學等眾多的工程與科學領域中得到廣泛套用,尤其是在電路理論的研究中,在相當長的時期內,人們幾乎無法把電路理論與拉普拉斯變換分開來討論。
定義
將系統中獨立變數是復頻率s的範圍,稱為s域,也稱復頻域。
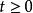 s域
s域 s域
s域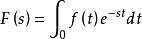 s域
s域 s域
s域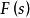 s域
s域當 時, 有定義,且積分 存在,則稱 為 的拉氏變換。
性質
線性性質
兩個函式代數和的拉氏變換等於兩個函式拉氏變換的代數和。
比例性質
K倍原函式的拉氏變換等於原函式拉氏變換的K倍。
微分性質
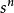 s域
s域在初始條件為零的前提下,原函式的n階導數的拉氏變換式等於其象函式乘以,使函式的微分運算變得十分簡單。
積分性質
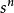 s域
s域在零初始條件下,原函式的n重積分的拉氏式等於其象函式除以,它是微積分的逆運算。
優點
拉氏變換分別將微分與積分運算轉換為乘法和除法運算;
指數函式、超越函式以及有不連續點的函式經拉氏變換可轉換為簡單的初等函式;
拉氏變換把時域中兩函式的卷積運算轉換為S域中兩函式的乘法運算;
利用系統函式零點、極點分布可以簡明、直觀地表達系統性能的許多規律;