定義
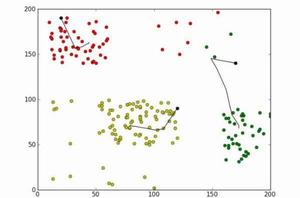
聚類是一個將數據集中在某些方面相似的數據成員進行分類組織的過程,聚類就是一種發現這種內在結構的技術,聚類技術經常被稱為無監督學習。
k均值聚類是最著名的劃分聚類算法,由於簡潔和效率使得他成為所有聚類算法中最廣泛使用的。給定一個數據點集合和需要的聚類數目k,k由用戶指定,k均值算法根據某個距離函式反覆把數據分入k個聚類中。
算法
先隨機選取K個對象作為初始的聚類中心。然後計算每個對象與各個種子聚類中心之間的距離,把每個對象分配給距離它最近的聚類中心。聚類中心以及分配給它們的對象就代表一個聚類。一旦全部對象都被分配了,每個聚類的聚類中心會根據聚類中現有的對象被重新計算。這個過程將不斷重複直到滿足某個終止條件。終止條件可以是以下任何一個:
1)沒有(或最小數目)對象被重新分配給不同的聚類。
2)沒有(或最小數目)聚類中心再發生變化。
3)誤差平方和局部最小。
偽代碼
選擇k個點作為初始質心。
repeat 將每個點指派到最近的質心,形成k個簇 重新計算每個簇的質心 until 質心不發生變化
性質
k均值聚類是使用最大期望算法(Expectation-Maximization algorithm)求解的高斯混合模型(Gaussian Mixture Model, GMM)在常態分配的協方差為單位矩陣,且隱變數的後驗分布為一組狄拉克δ函式時所得到的特例 。