基本介紹
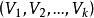 k臨界圖
k臨界圖 k臨界圖
k臨界圖 k臨界圖
k臨界圖 k臨界圖
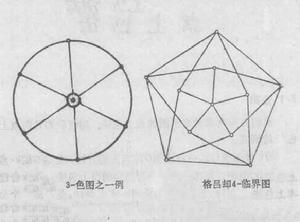
k臨界圖將k種顏色1,2,…,k塗到G的點上的方法,稱為G的 k-點 上色法,G的任二相鄰點均有不同顏色的點上色法,稱為 合理 點上色法。因而,無圈圖G的合理k-點上色法,是V的一個分劃 ,此處 為G的無關集(可能為空集)。若G有合理k-點上色法,則稱G為 可k-點上色圖。我們將合理點上色法,簡稱為上色法,合理k-點上色法,簡稱為k-上色法.同樣地,可k-點上色圖簡稱為可k-上色圖.顯然,圖為可k-上色圖若且唯若其精簡圖為可k-上色圖.因而研究圖的上色法時,我們只限於討論簡圖。簡圖為可1-上色圖若且唯若其為空圖,簡圖為可2-上色圖若且唯若其為二部圖.使G有k-上色法的最小自然數k,稱為G的 點色數或簡稱為G的 色數,記為 (G)。如果 (G)=k,稱G為k-色圖。圖1為一個3-色圖。實則,一個3-上色法已表示在圖1上。而且,因圖1不是二部圖,故無2-上色法。
 k臨界圖
k臨界圖 k臨界圖
k臨界圖討論所謂臨界圖的性質,對研究上色法是有用處的。圖G稱為臨界圖,如果對每一H⊂G,有 (H)< (G)。狄拉克於1952年首先研究這種圖。若圖G既為k-色圖又為臨界圖,則稱為 k-臨界圖。每一k-色圖有 k-臨界子圖。圖2為格呂卻(Grötzsch)的4-臨界圖。由臨界圖的定義,易知臨界圖是連通圖。
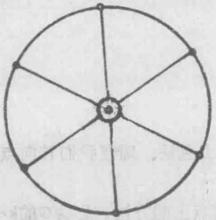 圖1
圖1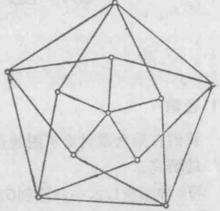 圖2
圖2相關性質
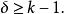 k臨界圖
k臨界圖定理1 若G為k-臨界圖,則
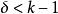 k臨界圖
k臨界圖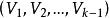 k臨界圖
k臨界圖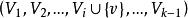 k臨界圖
k臨界圖證明 用反證法。若G為k-臨界圖,且 ,讓v是階數為δ的點,即d(v)=δ。因G為k-臨界圖,則G-v為可(k-1)-上色圖。設 是G-v的(k-1)-上色法。因d(v)=δ<k-1,故v必同某V的每一點都不相鄰。這樣一來, 為G的(k-1)-上色法,這同G為k-色圖矛盾 。
系1 k-色圖至少有k個點,它們都有階數≥k-1。
證明 讓G為k-色圖,H為G的k-臨界子圖,據定理1,若v∈V(H),則d(v)≥k-1。因而,d(v)≥k-1,又因H為k-色圖,故v(H)≥k。
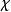 k臨界圖
k臨界圖系2 設G為(無圈)圖,則(G)≤Δ+1。
證明 由系1,即得結論。
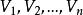 k臨界圖
k臨界圖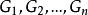 k臨界圖
k臨界圖讓S是連通圖G的點割集,且讓G-S的一切分支的點集為 ,則子圖G=G[V∪S]稱為G的S-分支(或S-連通支)(見圖3),在 上各給出一個上色法。若對每一v∈S,這n個上色法在n上均塗相同的顏色,則稱這n個上色法 在S上一致。
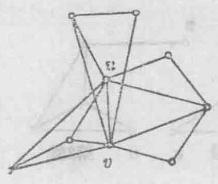 圖3(a) (a)G
圖3(a) (a)G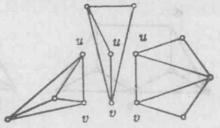 圖3(b) G的{u,v}-分支
圖3(b) G的{u,v}-分支定理2 讓G為臨界圖,若S⊂V(G)為G的點割集,則S不是G的完整集 。
系3 臨界圖為塊。
證明 若v為割裂點,則{v}為點割集,且亦為完整集。因而同定理2矛盾,所以,臨界圖為塊。
定理2的另一推論是,若k-臨界圖G有2-點割集{u,v},則u,v不相鄰.設G為k-臨界圖.我們稱G的{u,v}-分支G是第一型分支,如果G的每一(k-1)-上色法在u,v上塗相同顏色,稱G的{u,v}-分支G是第二型分支,若G的每一(k-1)-上色法在u,v上塗不同顏色(見圖4)。
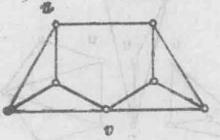 圖4(a)
圖4(a)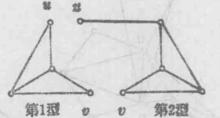 圖4(b)
圖4(b)定理3 (狄拉克,1953)讓G是k-臨界圖,且有2-點剖集{u,v},則
(i)G=G₁∪G₂,此處G是第i型(i=1,2){u,v}-分支;
(ii) G₁+uv和G₁ uv都是k-臨界圖。
系4 讓G是k-臨界圖,且{u,v}為其2-點割集,則
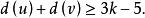 k臨界圖
k臨界圖