函式
Heaviside,符號法的創始人,工程師。heaviside函式是delta(x)函式從負無窮到x的積分;
簡介
在matlab的命令視窗中鍵入doc heaviside或者help heaviside可以獲得如下幫助信息:
“heaviside(x) has the value 0 for x < 0, 1 for x > 0, and 0.5 for x == 0. heaviside is not a function in the strict sense.”
即:
若令y=heaviside(x)
則當x<0時,y的值為0;當x>0時,y的值為1;當x等於0時,y=0.5。這是一個單位階躍函式。 從嚴格意義上來說,heaviside不是一個函式。(定義有誤heaviside仍然是函式,因為它是實數集到實數集的映射. 不過它不是連續函式.)
單位階躍函式的加窗特性套用很廣泛。
套用舉例
例一:
在matlab的命令視窗輸入:
>> heaviside(0) [Enter]
ans =
0.5000
這是Matlab 2011b中的結果在原來原點處值不存在的情況有所修改。
把下面的代碼寫到一個m檔案中,運行:
Y=[ ];
for x=-5:5
y=heaviside(x);
Y=[Y y];
end
Y
將在matlab的命令視窗中輸出:
Y =
0 0 0 0 0 NaN 1 1 1 1 1
例二:
下面將舉一個利用單位階躍函式加窗特性的例子:syms t y;
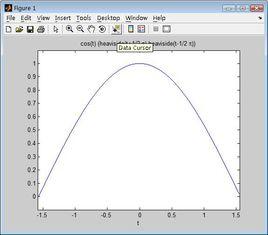
y=cos(t)*(heaviside(t+0.5*pi)-heaviside(t-0.5*pi));
ezplot(y);
這樣就可以獲得cos(t)在-pi/2<t<pi/2的波形。