簡介
經濟學家開拓了一種可以用來分析變數之間的因果的辦法，即 格蘭傑因果關係檢驗。該檢驗方法為2003年諾貝爾經濟學獎得主克萊夫·格蘭傑（Clive W. J. Granger）所開創，用於分析經濟變數之間的因果關係。他給因果關係的定義為“依賴於使用過去某些時點上所有信息的最佳最小二乘預測的方差。”
在時間序列情形下，兩個經濟變數X、Y之間的格蘭傑因果關係定義為：若在包含了變數X、Y的過去信息的條件下，對變數Y的預測效果要優於只單獨由Y的過去信息對Y進行的預測效果，即變數X有助於解釋變數Y的將來變化，則認為變數X是引致變數Y的格蘭傑原因。
進行格蘭傑因果關係檢驗的一個前提條件是時間序列必須具有平穩性，否則可能會出現虛假回歸問題。因此在進行格蘭傑因果關係檢驗之前首先應對各指標時間序列的平穩性進行單位根檢驗（unit root test)。常用增廣的迪基—富勒檢驗(ADF檢驗)來分別對各指標序列的平穩性進行單位根檢驗。
當X時間序列的由於“格蘭傑原因”導致了Y序列，X序列在一段時間的遲滯後，引起了Y序列的大致重複（可見圖中箭頭所指示），則X序列可以作為未來序列Y的預測。
格蘭傑在2003年諾貝爾獲獎時曾提出，“很多人把格蘭傑因果關係用在了非經濟學領域，從而得出了很多‘荒唐’的結論”，“當然，很多‘荒唐’的論文也隨之出現”。
核心概念
過去值
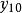granger因果檢驗
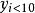granger因果檢驗過去值（lag value，或稱落後期）：同一變項比當期時間上更早的值。例如：當期為 ，它的落後期為 。
格蘭傑因果關係檢驗的基本觀念在於：未來的事件不會對目前與過去產生因果影響，而過去的事件才可能對現在及未來產生影響。也就是說，如果我們試圖探討變數x是否對變數y有因果影響，那么只需要估計x的落後期是否會影響y的現在值，因為x的未來值不可能影響y的現在值。假如在控制了y變數的過去值以後，x變數的過去值仍能對Y 變數有顯著的解釋能力，我們就可以稱x能“Granger 影響”（Granger-cause）y。
局限性和改進
最初版的格蘭傑因果測試，有時候無法發現真正的因果關係。因為雖然對於認定因果關係而言，理論上還必須控制其他可能的干擾因素，但在 Granger 最初提出這套因果測試的版本中，並未納入干擾變數的分析，而是假設其他可能解釋變數的資訊包含在y的落後值中。如果事實上帶來因果關係的是第三變數（干擾變數），亦即若事實上操控x並無法改變y，格蘭傑因果關係的零假設仍然可能被拒絕。因此標準版的格蘭傑因果測試結果可能會產生誤導性。
1980年代由其他的計量經濟學家對Granger測試加以修改、擴充，將可能的第三（以上）變數納入測試，成為使用面板資料的向量自回歸模型（英語：panel data VAR model）。相較於最初版的 Granger 測試，擴充版可以產生更有效的估計結果。
步驟描述
準備工作：一開始要用幾個落後期來建立模型，需要研究者的評估，通常使用赤池信息量準則（英語：Akaike information criterion、簡稱AIC） 或貝斯信息量準則（英語：Bayesian information criterion、簡稱BIC）來判斷。
格蘭傑因果關係檢驗的第一步是建立用y的落後期來預測y的自回歸模型。此際，如果時間序列y是廣義平穩的，則可以直接使用落後期。如果不平穩，就必須對不平穩的時間序列先做（一階或更多階）差分，直到得出平穩時間數列。
如果發現y的某期落後期 (1) 在回歸分析中具有顯著性（根據t檢定的p值來判斷），且 (2) 這期落後期加入模型後可提高回歸模型的解釋力（根據回歸分析的F檢定），這個落後期便被留在模型中。
然後進一步加入x（或Δx）的滯後期來擴充回歸模型。關於平穩時間序列的要求、某期落後期留在模型中的條件，同上述y的處理。
若且唯若（充分必要）沒有任何解釋變項x（或Δx）的落後期被留在模型中，便無法拒絕無格蘭傑因果關係的零假設。
1.準備工作：一開始要用幾個落後期來建立模型，需要研究者的評估，通常使用赤池信息量準則（英語：Akaike information criterion、簡稱AIC） 或貝斯信息量準則（英語：Bayesian information criterion、簡稱BIC）來判斷。
2.格蘭傑因果關係檢驗的第一步是建立用y的落後期來預測y的自回歸模型。此際，如果時間序列y是廣義平穩的，則可以直接使用落後期。如果不平穩，就必須對不平穩的時間序列先做（一階或更多階）差分，直到得出平穩時間數列。
3.如果發現y的某期落後期 (1) 在回歸分析中具有顯著性（根據t檢定的p值來判斷），且 (2) 這期落後期加入模型後可提高回歸模型的解釋力（根據回歸分析的F檢定），這個落後期便被留在模型中。
4.然後進一步加入x（或Δx）的滯後期來擴充回歸模型。關於平穩時間序列的要求、某期落後期留在模型中的條件，同上述y的處理。
5.若且唯若（充分必要）沒有任何解釋變項x（或Δx）的落後期被留在模型中，便無法拒絕無格蘭傑因果關係的零假設。
研究人員希望發現明顯的證據，比如x是y的格蘭傑原因但反之不成立，便能做出因果關係的推論。然而在實際操作中也可能會發現沒有變數是對方的格蘭傑原因，或者x和y兩個變數互為格蘭傑原因。
數學定義
1. 令x和y為廣義平穩序列。如要檢測x非y的格蘭傑原因之零假設，首先引入y的落後期建立y的自回歸模型（AR model ony）：
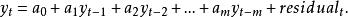granger因果檢驗所有的y落後期中：(1) 在回歸分析中具有顯著性（根據t-統計值的p值來判斷）的，且 (2) 這期落後期加入模型後可提高回歸模型的解釋力（根據回歸分析的F檢定）的－－將被留在模型中。m表示的是y變數滯後期中檢定為顯著的時間上最早一個。
2. 接著，引入x的落後期建立增廣回歸模型：
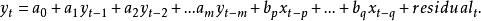granger因果檢驗所有的{\displaystyle x}落後期中：(1) 在回歸分析中具有顯著性（根據學生t檢驗的p值來判斷）的，且 (2) 這期落後期加入模型後可提高回歸模型的解釋力（根據回歸分析的F檢定）的－－將被留在模型中。在以上增廣回歸模型中，p代表x變數落後期中檢定為顯著的時間上最早一個，q則是x變數落後期中檢定為顯著的時間上最近一個。
3. 如果 沒有任何x的落後期被留在模型中，無格蘭傑因果關係的零假設就成立。
延伸
承繼著回歸模型的基本性質，格蘭傑因果關係分析也假設實際值與預測值之間的誤差呈常態分配，若實際現象不呈常態分配將嚴重影響推論的有效性。
Hacker & Hatemi-J (2006)發展出一種不必在乎誤差項是否呈常態分配的格蘭傑因果關係研究方法。這種方法在財金分析上特別實用， 因為許多金融變數不服從常態分配。
近來，Hacker & Hatemi-J (2012)又進一步改善之，提出一種非對稱的因果關係檢驗模型，據說可以區分正向與負向影響的因果影響。
