簡介
Box-Cox變換的一般形式為:
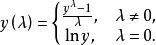 box-cox變換
box-cox變換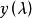 box-cox變換
box-cox變換 box-cox變換
box-cox變換 box-cox變換
box-cox變換 box-cox變換
box-cox變換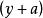 box-cox變換
box-cox變換 box-cox變換
box-cox變換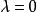 box-cox變換
box-cox變換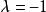 box-cox變換
box-cox變換 box-cox變換
box-cox變換 box-cox變換
box-cox變換式中為經Box-Cox變換後得到的新變數,為原始連續因變數,為變換參數。以上變換要求原始變數取值為正,若取值為負時,可先對所有原始數據同加一個常數使其為正值,然後再進行以上的變換。對不同的所作的變換不同。在時該變換為對數變換,時為倒數變換,而在時為平方根變換。Box-Cox變換中參數的估計有兩種方法:(1)最大似然估計;(2)Bayes方法。通過求解值,就可以確定具體採用哪種變換形式。
變換過程
Box-Cox變換是對回歸因變數Y的如下變換:
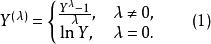 box-cox變換
box-cox變換 box-cox變換
box-cox變換 box-cox變換
box-cox變換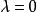 box-cox變換
box-cox變換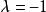 box-cox變換
box-cox變換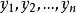 box-cox變換
box-cox變換在這裡是一個待定變換參數。對於不同的,所作的變換也不相同,所以Box-Cox變換是一族變換,它包括了平方根變換(),對數變換()和倒數變換()等常用變換,對因變數的n個觀測值,套用上述變換,可得變換後的向量
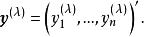 box-cox變換
box-cox變換 box-cox變換
box-cox變換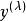 box-cox變換
box-cox變換我們要確定變換參數,使得滿足
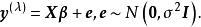 box-cox變換
box-cox變換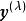 box-cox變換
box-cox變換 box-cox變換
box-cox變換即要求通過因變數的變換,使得變換過的向量與回歸自變數具有線性相依關係,誤差也服從常態分配.誤差各分量是等方差且相互獨立,故Box-Cox變換是通過參數的適當選擇。達到對原來數據的“綜合治理”,使其滿足一個正態線性回歸模型的所有假設條件。
 box-cox變換
box-cox變換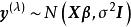 box-cox變換
box-cox變換 box-cox變換
box-cox變換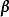 box-cox變換
box-cox變換 box-cox變換
box-cox變換用極大似然方法來確定,由於,故對固定的,和的似然函式為
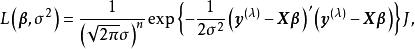 box-cox變換
box-cox變換 box-cox變換
box-cox變換其中,為變換的Jacobi行列式
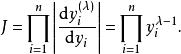 box-cox變換
box-cox變換 box-cox變換
box-cox變換 box-cox變換
box-cox變換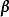 box-cox變換
box-cox變換 box-cox變換
box-cox變換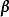 box-cox變換
box-cox變換 box-cox變換
box-cox變換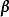 box-cox變換
box-cox變換 box-cox變換
box-cox變換當固定時,是不依賴於參數和的常數因子,的其餘部分關於和求導數,令其等於零,可求得和的極大似然估計
 box-cox變換
box-cox變換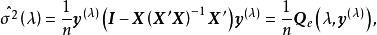 box-cox變換
box-cox變換殘差平方和為
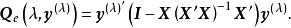 box-cox變換
box-cox變換對應的似然最大值為
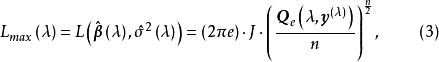 box-cox變換
box-cox變換 box-cox變換
box-cox變換 box-cox變換
box-cox變換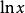 box-cox變換
box-cox變換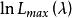 box-cox變換
box-cox變換 box-cox變換
box-cox變換該式為的一元函式,通過求它的最大值來確定,因為是x的單調函式,問題可轉化為求的最大值,對式(3)求對數,略去與無關的常數項,得
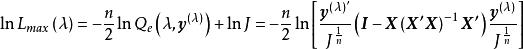 box-cox變換
box-cox變換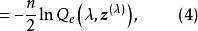 box-cox變換
box-cox變換其中,
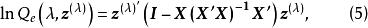 box-cox變換
box-cox變換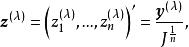 box-cox變換
box-cox變換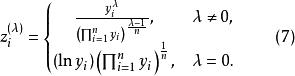 box-cox變換
box-cox變換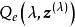 box-cox變換
box-cox變換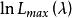 box-cox變換
box-cox變換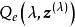 box-cox變換
box-cox變換 box-cox變換
box-cox變換 box-cox變換
box-cox變換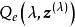 box-cox變換
box-cox變換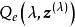 box-cox變換
box-cox變換 box-cox變換
box-cox變換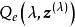 box-cox變換
box-cox變換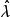 box-cox變換
box-cox變換式(4)對Box-Cox變換在計算機上實現帶來很大的方便,因為我們只要求出殘差平方和的最小值,就可以求出的最大值,雖然很難找出使達到最小值的的解析表達式,但是對一系列的給定值,通過最普通的求最小二乘估計的回歸程式,很容易計算出對應的,畫出關於的曲線,可在圖上近似地找出達到最小值的。
Box-Cox變換變換的具體步驟如下:
 box-cox變換
box-cox變換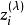 box-cox變換
box-cox變換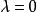 box-cox變換
box-cox變換(1)對給定的值,計算,如果,用式(6)計算,否則用式(7);
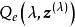 box-cox變換
box-cox變換(2)利用式(5)計算殘差平方和;
 box-cox變換
box-cox變換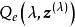 box-cox變換
box-cox變換 box-cox變換
box-cox變換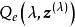 box-cox變換
box-cox變換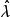 box-cox變換
box-cox變換(3)對一系列的值,重複上述步驟,得到相應的殘差平方和的一串值,以為橫軸,作出相應的曲線,用直觀的方法,找出使達到最小值的點。
(4)利用式(2),求出。
意義
 box-cox變換
box-cox變換Box-Cox變換的一個顯著優點是通過求變換參數來確定變換形式,而這個過程完全基於數據本身而無須任何先驗信息,這無疑比憑經驗或通過嘗試而選用對數、平方根等變換方式要客觀和精確。
Box-Cox變換的目的是為了讓數據滿足線性模型的基本假定,即線性、正態性及方差齊性,然而經Box-Cox變換後數據是否同時滿足了以上假定,仍需要考察驗證 。

