背景
布魯斯特角(也稱為偏振角)是具有特定偏振的光通過透明電介質表面完全透射而沒有反射的入射角。 因此當非偏振光以該角度入射時,從表面反射的光是完全極化的。 這種特殊的角度以蘇格蘭物理學家布魯斯特爵士(1781-1868)命名。
解釋
當光線以非垂直角度穿透光學元件(如分光鏡)的表面時,反射和透射特性均依賴於偏振現象。這種情況下,使用的坐標系是用含有輸入和反射光束的那個平面定義的。如果光線的偏振矢量在這個平面內,則稱為p-偏振,如果偏振矢量垂直於該平面,則稱為s-偏振。任何一種輸入偏振狀態都可以表示為s和p分量的矢量和。
當光線遇到具有不同折射率的兩種介質之間的邊界時,其中一些通常如下圖所示。反射由菲涅耳方程描述,並且取決於入射光的極化和入射角。
菲涅爾方程式預測,如果入射角為下式,則p-偏振光(在與入射光線相同的平面中極化的電場和表面法線)將不會被反射:
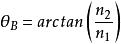 S偏振光
S偏振光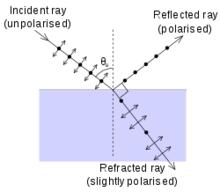 S偏振光
S偏振光其中n是光傳播入射介質的折射率,n是其他介質的折射率。 這個方程被稱為布魯斯特定律,由它定義的角度是布魯斯特角。
這種物理機制可以從介質中的電偶極子對p-偏振光的回響的方式定性地了解。 可以想像,入射在表面的光被吸收,然後通過在兩個介質之間的界面處振盪電偶極子再次輻射。 自由傳播光的偏振總是垂直於光線行進的方向。 產生透射(折射)光的偶極子在該光的偏振方向上振盪。 這些相同的振盪偶極子也產生反射光。 然而,偶極子不會在偶極矩的方向上輻射任何能量。 如果折射光被p-偏振並且正好垂直於預測光被鏡面反射的方向傳播,則偶極子沿著鏡面反射方向指向,因此不能反射光。 (見右圖)
用簡單的幾何關係,這個條件可以表示為:
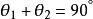 S偏振光
S偏振光其中θ是反射角(或入射角),θ是折射角。
使用斯奈爾定律,
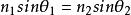 S偏振光
S偏振光可以計算沒有反射光的入射角θ=θ:
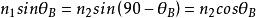 S偏振光
S偏振光解得θ:
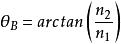 S偏振光
S偏振光對於空氣中的玻璃介質(n≈1.5)(n≈1),可見光的布魯斯特角度約為56°,而對於空氣-水界面(n≈1.33),布魯斯特角約為53°。由於給定介質的折射率根據光的波長而變化,因此布魯斯特角度也將隨波長而變化。
Étienne-Louis Malus在1808年首先觀察到光以特定角度從表面反射而被偏振的現象。他試圖將偏光角度與材料的折射率相關聯,但是由於當時的眼鏡質量不一致而導致試驗失敗。在1815年,布魯斯特實驗了更高質量的材料,並表明這個角度是折射率的函式,定義了布魯斯特定律。
布魯斯特角通常被稱為“偏振角”,因為從該表面以該角度反射的光完全偏離入射平面(“s極化”)。因此,可以將玻璃板或以布魯斯特角度放置在光束中的一疊平板作為偏振器。偏振角的概念可以擴展到布魯斯特波數的概念,以涵蓋兩個線性雙分散材料之間的平面界面。在布魯斯特角度反射的情況下,反射和折射的光線相互垂直。
對於磁性材料,布魯斯特角只能通過介電常數和磁導率的相對強度來確定入射波極化之一。這對於介電分界面的廣義布魯斯特角的存在有影響。
套用
偏光太陽鏡採用布魯斯特角度的原理,以減少從水面或道路等水平面反射的太陽光的眩光。 在布魯斯特角附近的大範圍的角度,p-偏振光的反射低於s-偏振光。 因此,如果太陽在天空很低,反射光主要是s極化的。 極化太陽鏡使用偏光材料如偏光片來阻擋水平偏振光,優先阻擋水平表面的反射。 效果最強,水面光滑,但道路和地面的反射也減少。
攝影師使用相同的原理去除水中的反射,以便他們可以拍攝表面下的物體。 在這種情況下,偏振濾鏡相機附屬檔案可以旋轉到正確的角度。
 S偏振光
S偏振光拍攝的照片帶有相機偏光鏡濾鏡旋轉到兩個不同的角度。 在左側的圖像中,偏振器與視窗反射的偏振角對準。 偏振器已旋轉90°,消除了極度偏振的反射太陽光(如上圖)。
當記錄全息圖時,光通常以布魯斯特角度入射。 因為入射光是p偏振的,所以它不會從全息膜的透明背面反射回來。 這樣可以避免全息圖中不必要的干涉效應。
布魯斯特角稜鏡用於雷射物理學。 偏振雷射以布魯斯特角進入稜鏡,沒有任何反射損失。
在表面科學中,布魯斯特角度顯微鏡用於空氣 - 液體界面處的顆粒或分子的成像層。 通過使用針對布魯斯特角度的雷射瞄準界面,純液體在圖像中顯得黑色,而分子層發出可以用相機檢測和呈現的反射。
偽布魯斯特角
當反射面吸收時,平行極化(p)的反射率在所謂的偽布魯斯特角處經過非零最小值。
