介紹
在數學最最佳化中， Rosenbrock函式是一個用來測試最最佳化算法性能的非凸函式，由Howard Harry Rosenbrock在1960年提出 。也稱為 Rosenbrock山谷或 Rosenbrock香蕉函式，也簡稱為 香蕉函式。
Rosenbrock函式的定義如下：
Rosenbrock函式Rosenbrock函式的每個等高線大致呈拋物線形，其全域最小值也位在拋物線形的山谷中（香蕉型山谷）。很容易找到這個山谷，但由於山谷內的值變化不大，要找到全域的最小值相當困難。其全域最小值位於 (x,y)=(1,1)點，數值為f(x,y)=0。有時第二項的係數不同，但不會影響全域最小值的位置。
多變數下的擴展
多變數的Rosenbrock函式有以下二種形式。一種是N/2個獨立二維Rosenbrock函式的和：
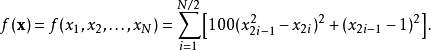Rosenbrock函式此形式只在N為偶數時有定義，而且其解較簡單。
另一個較複雜的形式為：
Rosenbrock函式
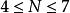Rosenbrock函式
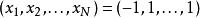Rosenbrock函式
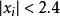Rosenbrock函式可證明當N=3時，此形式的Rosenbrock函式只有一個最小值（位置在 (1,1,1)），在 時只有二個最小值，所有變數均為1時有全域最小值，而在 附近有局部最小值。此結果是將令函式的梯度為0後求得，Rosenbrock函式的梯度仍為一個x的多項式，在N較小時，可以精確的列出多項式，再求出實根的個數，而其根限制在 的範圍內。 若N較大時因為相關的係數太多，無法用以上方式進行。
隨機函式
有許多方式可以將Rosenbrock函式延伸到隨機（stochastic）函式，以下是一種例子：
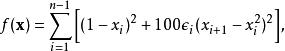Rosenbrock函式
Rosenbrock函式其中隨機變數 服從均勻分布Unif(0,1)。原則上，此隨機函式的全域最小值仍在(1,1,...,1)，不過因為其隨機的特性，任何以梯度下降法為基礎的最最佳化算法均無法用來求得此隨機函式的最小值。
可適用的最最佳化算法
經若經過適當的坐標系調整，可以在沒有梯度信息及不創建局部近似模型的情形下（和其他不使用梯度信息的最最佳化算法相反），用最最佳化算法求得Rosenbrock函式的最小值。
相關條目
•Himmelblau函式
•Rastrigin函式
•格里旺克函式
