概念
啟發式算法（heuristic algorithm)是相對於最最佳化算法提出的。一個問題的最優算法求得該問題每個實例的最優解。啟發式算法可以這樣定義：一個基於直觀或經驗構造的算法，在可接受的花費（指計算時間和空間）下給出待解決組合最佳化問題每一個實例的一個可行解，該可行解與最優解的偏離程度一般不能被預計。
而啟發式遺傳算法是將遺傳算法套用於啟發式算法中，用來解決最最佳化問題的一種算法。
遺傳算法與啟發式遺傳算法
遺傳算法
與其他啟發式搜尋方法一樣，遺傳算法在形式上是一種疊代方法，它從一組解（ 群體）出發，模擬生物體的進化機制，採用複製、交叉、變異等遺傳操作，在繼承原有優良基因的基礎上，生成具有更好性能指標的下一代解的群體，不斷疊代，直到搜尋到最優解或滿意解為止。用遺傳算法解決組合最佳化問題的一般步驟：
啟發式遺傳算法Step1： 確定群體規模i（整數）及遺傳操作的代數（整數）。初試代數k = 1，使用隨機方法或其他方法產生i個可能解 （ 1<=i<=n，k = 1）組成初始解群。
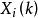啟發式遺傳算法
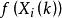啟發式遺傳算法Step2：對於群體中每一個個體 ，計算其適應度 。
Step3：while（！結束條件）
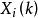啟發式遺傳算法
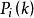啟發式遺傳算法對於群體中每一個體 ，計算其生存機率 ；
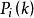啟發式遺傳算法根據生存機率 ，在群體中選擇父體執行遺傳操作，包括複製、交叉、變異，得到一個新的解群體，此時k = k + 1，轉第二步。
Step4：滿足條件，結束操作。
啟發式遺傳算法
遺傳算法是John Holland教授和他的學生們發展建立的 。早期的算法是簡單遺傳算法，效率很低。因此人們在套用遺傳算法時，常常對簡單遺傳算法進行修改，加入新技術，保留簡單遺傳算法的主要特點，同時又與之有所不同。
啟發式遺傳算法無約束最佳化問題非常適合遺傳算法，比方說求函式， 極大值問題。首先利用傳統數值解法提供初始群體；再用遺傳算法法則得到啟發式遺傳算法。啟發式遺傳算法的算法步驟 ：
啟發式遺傳算法 啟發式遺傳算法Step1：編碼表示。對於q維實向量 ，每一個分量都用一個二進制串表示，依照搜尋空聞確定串長l ，這樣每一點 的編碼由q個二進制串構成。
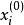啟發式遺傳算法
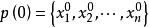啟發式遺傳算法Step2：選擇一個正整數n作為群體的規模參數，然後利用傳統數值解法生成n個近似最優點 (i=1，2…，n)，這些點構成初始群體 ，完成初始化。
Step3：給定一個很小的數M ，取適應值函式：
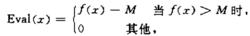啟發式遺傳算法
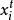啟發式遺傳算法計算第t代群體P(f)的每個個體 的適應值。
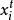啟發式遺傳算法Step4：對每個個體 計算其生存機率：
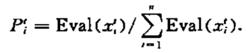啟發式遺傳算法 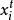啟發式遺傳算法然後根據隨機選擇策略，使得每個個體 被選擇進行演化。
啟發式遺傳算法
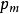啟發式遺傳算法Step5：對從群體P(t)中選擇複製的個體採用雜交運算元和變異運算元作用形成下一代新的個體，雜交是以機率 交換兩個父代個體間對應的分量。雜交完成後，再以最小機率 作用變異運算元。變異運算元是改變串中的等位基因。
Step6：循環執行第三、四、五步直到滿足停止準則，停止準則設定成最大代數或得到容許解時終止。
算法第三步中適應值函式的選取數M 是為了使適應值非負，這樣便於計算演化機率，顯然適應值越大目標函式越大，因而個體越優；反之，適應值越小的個體越差。適應值大的個體有更多的機會在下一代中再生。對於極小化問題可採取下面方法定義適應函式
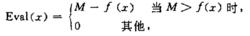啟發式遺傳算法啟發式遺傳算法的優勢
在科學實踐、工程技術和日常生活中， 人們常常會遇到大量的、各式各樣的最最佳化問題。最最佳化方法在近幾十年里獲得了巨大的發展，但目前很多方法不同程度上還存在著一些不足之處，尤其是最終所求得的大多為局部最優解，並不是全局最優解。而近年來得到蓬勃發展的遺傳算法其本質是一種求解問題的高效並行全局搜尋方法
。它能在搜尋過程中自動獲取和積累有關搜尋空間的知識，並自適應地控制搜尋過程以求得最優解。遺傳算法對目標函式或約束條件， 既不要求連續，又不要求可微， 只要問題是可計算的就行。儘管遺傳算法是一種全局隨機最佳化方法， 但它也存在缺點，主要是：
（1）完全依賴機率隨機地進行尋優操作雖然可以避免陷入局部極小， 但受尋優條件的限制， 一般只能得到全局範圍內的次優解，很難得到最優解；
（2）通過參數的二進制編碼字元串間接運算， 人為地將連續空間離散化， 導致計算精度與字元串長度、運算量之間的矛盾；
（3）由於遺傳算法採用隨機最佳化技術，所以要花費大量的時間；
（4）遺傳算法雖然具有很強的全局搜尋能力，但其局部搜尋能力較弱。
針對以上存在的問題，將遺傳算法與梯度尋優技術結合起來，並採用原始變數來構成染色體，設計出啟發式遺傳算法，可以成功解決上述問題。
套用
啟發式遺傳算法搜尋能力很強，下面給出了兩個具體套用 。
Camel函式的最最佳化問題
Camel函式：
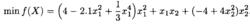啟發式遺傳算法
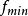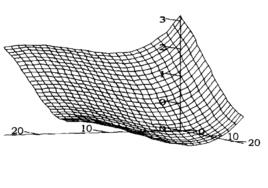
啟發式遺傳算法這是一個處處可導的函式, 存在有6 個局部極小點。最優點是（-0.0898，0.7126）和（0.0898，0.7126），最優解 =-1.031628，其圖像如下：
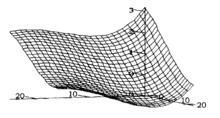啟發式遺傳算法
啟發式遺傳算法 啟發式遺傳算法將常規變異操作和啟發式遺傳算法中的變異操作兩種方式用於Camel函式的最最佳化問題，並比較和分析最佳化結果。表1 給出了對於10 個不同的初始解群， 取不同值並分別疊代200代時所達到的平均值，其中 =0 代表常規變異操作：
啟發式遺傳算法 啟發式遺傳算法由表1可見，在相同疊代次數下變異操作可以最佳化結果，但當 >=0.6時不如遺傳算法。
banana函式的最最佳化問題
由Rosenbrock設計的Banana函式是一個極難最佳化的函式，理論分析與數值計算表明，Banana函式對於最速下降法是不成功的，甚至在合理的時間內完全不收斂。
Banana函式定義為：
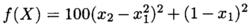啟發式遺傳算法 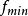啟發式遺傳算法最優解是X*=（1，1）， =0，函式曲面和等高線圖如圖：
啟發式遺傳算法通過實例計算表明，在遠離X*=（0，0）點的區域內任意選取10個初始解群，經過啟發式遺傳算法的搜尋，都能收斂到最小值點，平均值為：
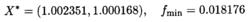啟發式遺傳算法從計算情況可知，在相同精度條件下，啟發式遺傳算法所用時間大概是遺傳算法的四分之一。
