基本含義
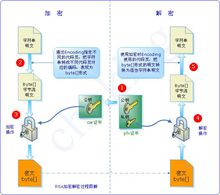 RSA算法
RSA算法 RSA公開密鑰密碼體制。所謂的公開密鑰密碼體制就是使用不同的加密密鑰與解密密鑰,是一種“由已知加密密鑰推導出解密密鑰在計算上是不可行的”密碼體制。
在公開密鑰密碼體制中,加密密鑰(即公開密鑰)PK是公開信息,而解密密鑰(即秘密密鑰)SK是需要保密的。加密算法E和解密算法D也都是公開的。雖然解密密鑰SK是由公開密鑰PK決定的,但卻不能根據PK計算出SK。
正是基於這種理論,1978年出現了著名的RSA算法,它通常是先生成一對RSA 密鑰,其中之一是保密密鑰,由用戶保存;另一個為公開密鑰,可對外公開,甚至可在網路伺服器中註冊。為提高保密強度,RSA密鑰至少為500位長,一般推薦使用1024位。這就使加密的計算量很大。為減少計算量,在傳送信息時,常採用傳統加密方法與公開密鑰加密方法相結合的方式,即信息採用改進的DES或IDEA對話密鑰加密,然後使用RSA密鑰加密對話密鑰和信息摘要。對方收到信息後,用不同的密鑰解密並可核對信息摘要。
RSA算法是第一個能同時用於加密和數字簽名的算法,也易於理解和操作。RSA是被研究得最廣泛的公鑰算法,從提出到現今的三十多年裡,經歷了各種攻擊的考驗,逐漸為人們接受,普遍認為是目前最優秀的公鑰方案之一。
SET(Secure Electronic Transaction)協定中要求CA採用2048bits長的密鑰,其他實體使用1024比特的密鑰。RSA密鑰長度隨著保密級別提高,增加很快。下表列出了對同一安全級別所對應的密鑰長度。
| 保密級別 | 對稱密鑰長度(bit) | RSA密鑰長度(bit) | ECC密鑰長度(bit) | 保密年限 |
| 80 | 80 | 1024 | 160 | 2010 |
| 112 | 112 | 2048 | 224 | 2030 |
| 128 | 128 | 3072 | 256 | 2040 |
| 192 | 192 | 7680 | 384 | 2080 |
| 256 | 256 | 15360 | 512 | 2120 |
RSA算法是一種非對稱密碼算法,所謂非對稱,就是指該算法需要一對密鑰,使用其中一個加密,則需要用另一個才能解密。這種算法1978年就出現了,它是第一個既能用於數據加密也能用於數字簽名的算法。它易於理解和操作,也很流行。算法的名字以發明者的名字命名:Ron Rivest, Adi Shamir 和 Leonard Adleman。早在1973年,英國國家通信總局的數學家Clifford Cocks就發現了類似的算法。但是他的發現被列為絕密,直到1998年才公諸於世。
RSA的算法涉及三個參數,n、e1、e2。
其中,n是兩個大質數p、q的積,n的二進制表示時所占用的位數,就是所謂的密鑰長度。
e1和e2是一對相關的值,e1可以任意取,但要求e1與(p-1)*(q-1)互質;再選擇e2,要求(e2*e1)mod((p-1)*(q-1))=1。
(n,e1),(n,e2)就是密鑰對。其中(n,e1)為公鑰,
RSA加解密的算法完全相同,設A為明文,B為密文,則:A=B^e2 mod n;B=A^e1 mod n;(公鑰加密體制中,一般用公鑰加密,私鑰解密)
e1和e2可以互換使用,即:
A=B^e1 mod n;B=A^e2 mod n;
安全性
RSA的安全性依賴於大數分解,但是否等同於大數分解一直未能得到理論上的證明,因為沒有證明破解 RSA就一定需要作大數分解。假設存在一種無須分解大數的算法,那它肯定可以修改成為大數分解算法。目前, RSA 的一些變種算法已被證明等價於大數分解。不管怎樣,分解n是最顯然的攻擊方法。現在,人們已能分解多個十進制位的大素數。因此,模數n 必須選大一些,因具體適用情況而定。
實現細節
密鑰生成
首先要使用機率算法來驗證隨機產生的大的整數是否質數,這樣的算法比較快而且可以消除掉大多數非質數。假如有一個數通過了這個測試的話,那么要使用一個精確的測試來保證它的確是一個質數。
除此之外這樣找到的p和q還要滿足一定的要求,首先它們不能太靠近,此外p-1或q-1的因子不能太小,否則的話N也可以被很快地分解。
此外尋找質數的算法不能給攻擊者任何信息,這些質數是怎樣找到的,尤其產生隨機數的軟體必須非常好。要求是隨機和不可預測。這兩個要求並不相同。一個隨機過程可能可以產生一個不相關的數的系列,但假如有人能夠預測出(或部分地預測出)這個系列的話,那么它就已經不可靠了。比如有一些非常好的隨機數算法,但它們都已經被發表,因此它們不能被使用,因為假如一個攻擊者可以猜出p和q一半的位的話,那么他們就已經可以輕而易舉地推算出另一半。
此外密鑰d必須足夠大,1990年有人證明假如p大於q而小於2q(這是一個很經常的情況)而,那么從N和e可以很有效地推算出d。此外e = 2永遠不應該被使用。
運算速度
由於進行的都是大數計算,使得RSA最快的情況也比DES慢上好幾倍,無論是軟體還是硬體實現。速度一直是RSA的缺陷。一般來說只用於少量數據加密。RSA的速度比對應同樣安全級別的對稱密碼算法要慢1000倍左右。
比起DES和其它對稱算法來說,RSA要慢得多。實際上Bob一般使用一種對稱算法來加密他的信息,然後用RSA來加密他的比較短的對稱密碼,然後將用RSA加密的對稱密碼和用對稱算法加密的訊息送給Alice。
這樣一來對隨機數的要求就更高了,尤其對產生對稱密碼的要求非常高,因為否則的話可以越過RSA來直接攻擊對稱密碼。
密鑰分配
和其它加密過程一樣,對RSA來說分配公鑰的過程是非常重要的。分配公鑰的過程必須能夠抵擋一個從中取代的攻擊。假設Eve交給Bob一個公鑰,並使Bob相信這是Alice的公鑰,並且她可以截下Alice和Bob之間的信息傳遞,那么她可以將她自己的公鑰傳給Bob,Bob以為這是Alice的公鑰。Eve可以將所有Bob傳遞給Alice的訊息截下來,將這個訊息用她自己的密鑰解密,讀這個訊息,然後將這個訊息再用Alice的公鑰加密後傳給Alice。理論上Alice和Bob都不會發現Eve在偷聽他們的訊息。今天人們一般用數字認證來防止這樣的攻擊。
時間攻擊
1995年有人提出了一種非常意想不到的攻擊方式:假如Eve對Alice的硬體有充分的了解,而且知道它對一些特定的訊息加密時所需要的時間的話,那么她可以很快地推導出d。這種攻擊方式之所以會成立,主要是因為在進行加密時所進行的模指數運算是一個位元一個位元進行的而位元為1所花的運算比位元為0的運算要多很多,因此若能得到多組訊息與其加密時間,就會有機會可以反推出私鑰的內容。
模數攻擊
若系統中共有一個模數,只是不同的人擁有不同的e和d,系統將是危險的。最普遍的情況是同一信息用不同的公鑰加密,這些公鑰共模而且互質,那么該信息無需私鑰就可得到恢復。設P為信息明文,兩個加密密鑰為e1和e2,公共模數是n,則:
C1 = P^e1mod n
C2 = P^e2 mod n
密碼分析者知道n、e1、e2、C1和C2,就能得到P。
因為e1和e2互質,故用Euclidean算法能找到r和s,滿足:
r * e1 + s * e2 = 1
假設r為負數,需再用Euclidean算法計算C1^(-1),則
(C1^(-1))^(-r) * C2^s = P mod n
另外,還有其它幾種利用公共模數攻擊的方法。總之,如果知道給定模數的一對e和d,一是有利於攻擊者分解模數,一是有利於攻擊者計算出其它成對的e’和d’,而無需分解模數。解決辦法只有一個,那就是不要共享模數n。
RSA的小指數攻擊。有一種提高 RSA速度的建議是使公鑰e取較小的值,這樣會使加密變得易於實現,速度有
所提高。但這樣作是不安全的,對付辦法就是e和d都取較大的值。
RSA的邊信道攻擊
針對RSA的邊信道攻擊現今大多處於實驗室階段,邊信道攻擊並不是直接對RSA的算法本身進行攻擊,而是針對計算RSA的設備的攻擊。現今的邊信道攻擊一般是針對硬體實現RSA算法的晶片進行的。
現國內外防範公鑰密碼邊信道攻擊主要以犧牲效率為代價。公鑰密碼的實現效率一直是信息安全系統的套用瓶頸,進一步損害算法效率,必將造成信息系統性能惡化。因此,尋找高效又抗功耗分析的公鑰算法實現途徑,並結合其他層面抗攻擊手段,使密碼器件運行效率、功耗、面積等綜合因素實現最最佳化,無疑是極富挑戰性的課題,不僅對抗邊信道攻擊理論研究有重要價值,而且對廣泛套用的智慧卡(尤其是銀行卡、手機SIM或USIM卡)、各種硬體密碼電子設備、有時也包括軟體實現的密碼算法的安全套用無疑具有極大的現實意義。
邊信道攻擊以功耗分析和公鑰密碼為研究重點,在對各種類型、系列、型號、規模的基本電路運行過程中的功耗軌跡進行大量研究、掌握其變化規律的基礎上,繼續研究電路工藝、結構、算法、協定對功耗軌跡的影響,經過一系列處理,從中提取出密鑰信息。目標是針對功耗分析攻擊機理,提出抗功耗分析的綜合最佳化新方法,並儘量兼顧算法效率。
邊信道攻擊研究涉及密碼學、資訊理論、算法理論和噪聲理論,還涉及硬體電路設計、通信、信號處理、統計分析、模式識別等諸多技術。
邊信道攻擊在若干關鍵問題研究上已取得了實質性進展。
目前國內已經有大學的研究者提出了公鑰密碼等功耗編碼的綜合最佳化方法,佐證了安全性和效率的可兼顧性。截至目前,研究團隊已針對著名公鑰密碼算法RSA的多種實現算法和方式成功實施了計時攻擊、簡單功耗和簡單差分功耗分析攻擊,實驗驗證了多種防禦方法,包括 “等功耗編碼”方法的有效性,並完成了大規模功耗分析自動測試平台的自主開發。
攻擊進度
針對RSA最流行的攻擊一般是基於大數因數分解。1999年,RSA-155(512bits)被成功分解,花了五個月時間(約8000 MIPS 年)和224 CPU hours 在一台有3.2G中央記憶體的Cray C916計算機上完成。
2002年,RSA-158也被成功因數分解。
2009年12月12日,編號為 RSA-768 (768bits,232 digits)數也被成功分解。
台北時間2013年2月15日上午訊息,據《紐約時報》周二報導,歐美數學家和密碼學家偶然發現,被全世界廣泛套用的公鑰加密算法RSA存在漏洞。
他們發現,在700萬個實驗樣本中有2.7萬個公鑰並不是按理論隨機產生的。也就是說,或許有人可以找出產生公鑰的秘密質數。
該研究項目是由美國獨立密碼學家James P.Hughes和荷蘭數學家Arjen K. Lenstra牽頭的。他們的報告稱:“我們發現絕大多數公鑰都是按理論產生的,但是每一千個公鑰中會有兩個存在安全隱患。”
報告稱,為防止有人利用該漏洞,有問題的公鑰已從公眾訪問的資料庫中移除。為確保系統的安全性,網站需要在終端做出改變。
公式和定理
數和互為素數
任何大於1的整數a能被因式分解為如下唯一形式:
a=p1p2…pl(p1,p2,…,pl為素數)
二、模運算
①{[a(mod n)]×[b(mod n)]}modn≡(a×b)(mod n)
②如果(a×b)=(a×c)(mod n),a與n互素,則
b=c(mod n)
三、費馬定理若p是素數,a與p互素,則
a^(p-1)≡1 (mod p)
四、歐拉定理
歐拉函式φ(n)表示不大於n且與n互素的正整數的個數。
當n是素數,φ(n)=n-1。n=pq,p,q均為素數時,則φ(n)= φ(p)φ(q)=(p-1)(q-1)。
對於互素的a和n,有a^φ(n)≡1(mod n)
如何利用電腦程式從公鑰e,以及φ(n)求得私鑰d?
問題可以化為求: e *x +φ(n)* y = 1 類型的方程,利用擴展歐幾里得算法求解
c++實現
Java實現詳細案例:
java實現

