基本簡介
 PID算法
PID算法控制點目前包含三種比較簡單的PID控制算法,分別是:增量式算法,位置式算法,微分先行。 這三種PID算法雖然簡單,但各有特點,基本上能滿足一般控制的大多數要求。
算法種類
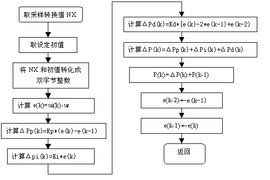
PID增量式算法
離散化公式:
△u(k)= u(k)- u(k-1)
△u(k)=Kp[e(k)-e(k-1)]+Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)]
 PID儀表
PID儀表進一步可以改寫成
△u(k)=Ae(k)-Be(k-1)+Ce(k-2)
對於增量式算法,可以選擇的功能有:
(1) 濾波的選擇
可以對輸入加一個前置濾波器,使得進入控制算法的給定值不突變,而是有一定慣性延遲的緩變數。
(2) 系統的動態過程加速
在增量式算法中,比例項與積分項的符號有以下關係:如果被控量繼續偏離給定值,則這兩項符號相同,而當被控量向給定值方向變化時,則這兩項的符號相反。
由於這一性質,當被控量接近給定值的時候,反號的比例作用阻礙了積分作用,因而避免了積分超調以及隨之帶來的振盪,這顯然是有利於控制的。但如果被控量遠未接近給定值,僅剛開始向給定值變化時,由於比例和積分反向,將會減慢控制過程。
為了加快開始的動態過程,我們可以設定一個偏差範圍v,當偏差|e(t)|< β時,即被控量接近給定值時,就按正常規律調節,而當|e(t)|>= β時,則不管比例作用為正或為負,都使它向有利於接近給定值的方向調整,即取其值為|e(t)-e(t-1)|,其符號與積分項一致。利用這樣的算法,可以加快控制的動態過程。
(3) PID增量算法的飽和作用及其抑制
在PID增量算法中,由於執行元件本身是機械或物理的積分儲存單元,如果給定值發生突變時,由算法的比例部分和微分部分計算出的控制增量可能比較大,如果該值超過了執行元件所允許的最大限度,那么實際上執行的控制增量將時受到限制時的值,多餘的部分將丟失,將使系統的動態過程變長,因此,需要採取一定的措施改善這種情況。
糾正這種缺陷的方法是採用積累補償法,當超出執行機構的執行能力時,將其多餘部分積累起來,而一旦可能時,再補充執行。
PID位置算法
離散公式:
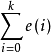 PID算法
PID算法u(k)=Kp*e(k) +Ki*
+Kd*[e(k)-e(k-1)]
對於位置式算法,可以選擇的功能有:
a、濾波:同上為一階慣性濾波
b、飽和作用抑制:
遇限削弱積分法
一旦控制變數進入飽和區,將只執行削弱積分項的運算而停止進行增大積分項的運算。具體地說,在計算Ui時,將判斷上一個時刻的控制量Ui-1是否已經超出限制範圍,如果已經超出,那么將根據偏差的符號,判斷系統是否在超調區域,由此決定是否將相應偏差計入積分項。
積分分離法
在基本PID控制中,當有較大幅度的擾動或大幅度改變給定值時, 由於此時有較大的偏差,以及系統有慣性和滯後,故在積分項的作用下,往往會產生較大的超調量和長時間的波動。特別是對於溫度、成份等變化緩慢的過程,這一現象將更嚴重。為此可以採用積分分離措施,即偏差較大時,取消積分作用;當偏差較小時才將積分作用投入。
另外積分分離的閾值應視具體對象和要求而定。若閾值太大,達不到積分分離的目的,若太小又有可能因被控量無法跳出積分分離區,只進行PD控制,將會出現殘差。
離散化公式:
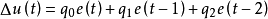 PID算法
PID算法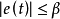 PID算法
PID算法當
時
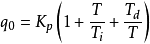 PID算法
PID算法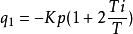 PID算法
PID算法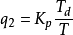 PID算法
PID算法當|e(t)|>β時
q0 = Kp(1+Td/T)
q1 = -Kp(1+2Td/T)
q2 = Kp Td /T
u(t) = u(t-1) + Δu(t)
註:各符號含義如下
u(t);;;;; 控制器的輸出值。
e(t);;;;; 控制器輸入與設定值之間的誤差。
Kp;;;;;;; 比例係數。
Ti;;;;;;; 積分時間常數。
Td;;;;;;; 微分時間常數。(有的地方用"Kd"表示)
T;;;;;;;; 調節周期。
β;;;;;;; 積分分離閾值
有效偏差法
當根據PID位置算法算出的控制量超出限制範圍時,控制量實際上只能取邊際值U=Umax,或U=Umin,有效偏差法是將相應的這一控制量的偏差值作為有效偏差值計入積分累計而不是將實際的偏差計入積分累計。因為按實際偏差計算出的控制量並沒有執行。
如果實際實現的控制量為U=U(上限值或下限值),則有效偏差可以逆推出,即:
=
然後,由該值計算積分項
微分先行PID算法
當控制系統的給定值發生階躍時,微分作用將導致輸出值大幅度變化,這樣不利於生產的穩定操作。因此在微分項中不考慮給定值,只對被控量(控制器輸入值)進行微分。微分先行PID算法又叫測量值微分PID算法。公式如下:
離散化公式:
參數說明同上
對於純滯後對象的補償
控制點採用了Smith預測器,使控制對象與補償環節一起構成一個簡單的慣性環節。
PID參數整定
(1) 比例係數Kp對系統性能的影響
:
比例係數加大,使系統的動作靈敏,速度加快,穩態誤差減小。Kp偏大,振盪次數加多,調節時間加長。Kp太大時,系統會趨於不穩定。Kp太小,又會使系統的動作緩慢。Kp可以選負數,這主要是由執行機構、感測器以控制對象的特性決定的。如果Kc的符號選擇不當對象狀態(pv值)就會離控制目標的狀態(sv值)越來越遠,如果出現這樣的情況Kp的符號就一定要取反。
(2) 積分控制Ti對系統性能的影響
:
積分作用使系統的穩定性下降,Ti小(積分作用強)會使系統不穩定,但能消除穩態誤差,提高系統的控制精度。
(3) 微分控制Td對系統性能的影響
:
微分作用可以改善動態特性,Td偏大時,超調量較大,調節時間較短。Td偏小時,超調量也較大,調節時間也較長。只有Td合適,才能使超調量較小,減短調節時間。