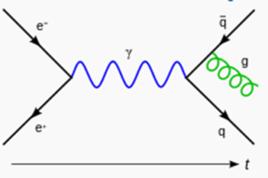
基本介紹
微觀高能物理實驗中,我們實際上對相互作用的細節無法測量。我們只知道反應前的粒子數(亮度)和反應後的末態數,實際表現為反應截面和衰變寬度。它們都由S矩陣元來表達。因此實際的物理觀測量是S矩陣元。通過理論計算S矩陣元(用物理量如質量、耦合常數等)來表達。也就是說,通過對S矩陣元的實驗測量和理論計算,我們才可以了解相互作用的本質。
那么理論計算的核心就是計算S矩陣元。歷史上,Lehnamn,Symanzik和Zimmermann首先在場論框架下推導出了S矩陣元和場算符的關聯函式(格林函式)的關係,現在將這種聯繫統稱為LSZ約化公式。 相對而言,格林函式在場論中有很好的定義,是場論的更基本的物理量,包含了理論體系的所有性質。
具體而言,如果我們要計算2-body→n-body過程的S矩陣元,我們可以計算相應的n+2個Heisenberg場算符的關聯函式。這些關聯函式的動量空間表達在p 復空間存在極點,這些極點可以理解為對應物理態,即漸進態,它們在無窮遠的過去和將來是自由的物理粒子態。多極點(比如n+2個極點)項的係數(留數)就是我們需要的S矩陣元。
不同場的約化公式
標量場的LSZ約化公式
 LSZ約化公式
LSZ約化公式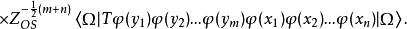 LSZ約化公式
LSZ約化公式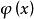 LSZ約化公式
LSZ約化公式:海森堡算符(相互作用理論中的算符);
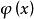 LSZ約化公式
LSZ約化公式Z:場算符 的波函式正比常數;
m:物理質量;
Ω:物理真空。
Dirac場的LSZ約化公式
 LSZ約化公式
LSZ約化公式動態電子態 :
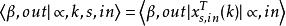 LSZ約化公式
LSZ約化公式 LSZ約化公式
LSZ約化公式 LSZ約化公式
LSZ約化公式動態正電子態 :
 LSZ約化公式
LSZ約化公式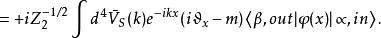 LSZ約化公式
LSZ約化公式 LSZ約化公式
LSZ約化公式末態電子態 :
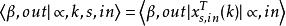 LSZ約化公式
LSZ約化公式 LSZ約化公式
LSZ約化公式 LSZ約化公式
LSZ約化公式末態正電子態 :
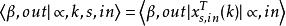 LSZ約化公式
LSZ約化公式 LSZ約化公式
LSZ約化公式初末態包含光子的LSZ約化公式
 LSZ約化公式
LSZ約化公式末態包含一個光子
 LSZ約化公式
LSZ約化公式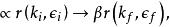 LSZ約化公式
LSZ約化公式末態包含一個光子,初態包含一個光子
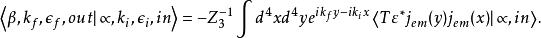 LSZ約化公式
LSZ約化公式微擾論——格林函式的微擾計算
在LSZ約化公式中出現的是海森堡場(相互作用場)算符關聯函式(格林函式),即它們的編時乘積在物理真空態之間的矩陣元:
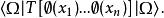 LSZ約化公式
LSZ約化公式對於相互有相互作用的理論,很難對它們進行直接的解析計算。
格點場論(Lattice Field Theory)可以對它們進行數值模擬計算(採用路徑積分量子化形式)。
但是,如果相互作用耦合常數比較小,相互作用Hamiltonian可以看作微擾項,則可以採用對相互作用項進行微擾展開。
格林函式在相互作用表象中(場是自由場,滿足自由場運動方程)可以表示為:
 LSZ約化公式
LSZ約化公式這是微擾論計算的出發點。