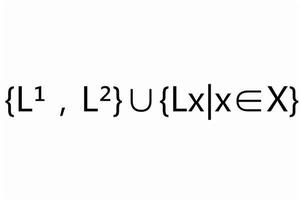基本介紹
設X為n元集,L¹與L²分別為X上的正交表OA(n,4),對每個x∈X,L是X\{x}上的正交表OA(n-1,3)(見下文“正交陣列”)。若存在c∈X,使對任一x∈X有(x,x,x,c)∈L¹∩L²,且對任一(u,v,w)∈X³,或存在x∈X使(u,v,w)∈L,或存在t∈X及j∈{1,2}使(u,v,w,t)∈L ,則稱{L¹,L²}∪{L|x∈X}為LD設計,記為LD(n)。這類設計對施泰納三元系大集問題有重要作用,對別的組合設計的存在性問題也有用,LD(n)的存在性已基本解決,除十幾個n值外LD(n)都是存在的 。
正交陣列
正交陣列即正交表,正交陣列是一類組合設計,設A是v元集X上的v×k矩陣,若對任意d(2≤d≤k)列所構成的子矩陣,X上的每一個d元排列作為子矩陣的行各出現λ次,則稱A為大小N,約束數k,水平數v,強度d和指數λ的正交陣列,在試驗設計中稱正交表,記為OA(N,k,v,d),由定義有N=λv ,強度2的正交陣列記為OA(v,k;λ),當λ=1時簡記為OA(v,k).OA(v,k;λ)的存在性等價於橫截設計TD[k;v]的存在性,OA(v,k)的存在性則等價於k-2個v階相互正交拉丁方的存在性 。
相關介紹
關於施泰納三元系大集的研究
陸家羲是獲得國家自然科學獎一等獎中唯一的一位普通中學教師。他解決的STEINER三元系大集問題屬於組合數學的設計理論領域,是19世紀50年代由Cayley、Sylvester和Kirkman等人提出來的,在組合設計的理論和套用上有重要意義,但是由於問題本身的艱難性,直至本世紀70年代進展甚微。自1972年始,國外一些組合設計學家引進逆推方法,對它有了部分推進,但直到1980年止,結果依然是零碎的,距完全解決相去甚遠。陸家羲經過20多年的刻苦鑽研,終於在1981-1983年基本上解決了這一難題,對所余的6個未定數值也給出了解決框架。國際組合數學刊物於1981年9月和1983年4月分兩期登載了他為解決這個問題所寫的6篇文章。這一成果獲1987年第三次國家自然科學獎一等獎。
1981-1983年,陸家羲以16個引理29個定理,嚴謹地布下整體解決問題的格局,引人各一個遞歸構造,獨創了一系列的輔助設計,運用前人已有的各種結論進行了複雜的計算和歸納,最終證明大集定理:
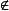 LD設計
LD設計如果v≡1,3(mod 6),v>7,和v{141,283,501,789,1 501,2 305},那么D(v)=v-2,人們還編成大集定理的算法程式,在計算機上驗證了大集定理的結論是完全正確的。
陸家羲的這一成果已載入組合數學史冊。