定義
在基於網路屬性模擬的生成模型中,有一些模型使用矩陣的乘積模擬網路的鄰接矩陣的擴展和演化。其中,Jure Leskovec等研究人員發現可以用矩陣的Kronecker乘積操作來生成網路,並且通過實驗驗證了Kronecker圖模型生成的網路可以很好地模擬靜態網路的度分布、特徵值分布以及動態網路的直徑、密度變化的冪律分布等特性。Kronecker積的數學特性使得Kronecker圖模型所生成的網路具有良好的可分析性。
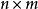 Kronecher模型
Kronecher模型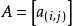 Kronecher模型
Kronecher模型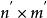 Kronecher模型
Kronecher模型 Kronecher模型
Kronecher模型 Kronecher模型
Kronecher模型 Kronecher模型
Kronecher模型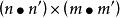 Kronecher模型
Kronecher模型 Kronecher模型
Kronecher模型Kronecker積是一種矩陣乘積運算。給定大小為 的矩陣 和大小為 的矩陣 ,那么矩陣 和 的Kronecker積表示一個大小為 的矩陣 ,並且
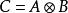 Kronecher模型
Kronecher模型套用
由上式可以看到,不同於矩陣的其他乘法,矩陣的Kronecker積是矩陣的擴展操作。那么,將兩個圖之間的Kronecker積定義為它們的鄰接矩陣的Kronecker積,就可以進行圖的擴展操作,並且擴展生成的圖具有自相似的特性,如下圖所示:
 Kronecher模型
Kronecher模型 Kronecher模型
Kronecher模型1)具有三個節點的鏈圖。
2)Kronecker積的中間狀態,表示節點擴展後的結果。
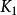 Kronecher模型
Kronecher模型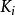 Kronecher模型
Kronecher模型 Kronecher模型
Kronecher模型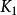 Kronecher模型
Kronecher模型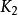 Kronecher模型
Kronecher模型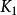 Kronecher模型
Kronecher模型3)的自Kronecker積結果。用表示個的Kronecker積。特別地,表示兩個的Kronecker積。
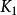 Kronecher模型
Kronecher模型4)的鄰接矩陣。
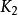 Kronecher模型
Kronecher模型5)的鄰接矩陣。
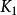 Kronecher模型
Kronecher模型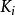 Kronecher模型
Kronecher模型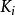 Kronecher模型
Kronecher模型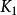 Kronecher模型
Kronecher模型 Kronecher模型
Kronecher模型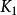 Kronecher模型
Kronecher模型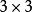 Kronecher模型
Kronecher模型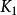 Kronecher模型
Kronecher模型Kronecker圖模型的網路生成過程就是對一個初始圖,進行多次Kronecker積操作,最終形成。易知的規模為規模的次冪。根據Kronecker積的作用過程可以得知,即使的規模非常小,如的矩陣,最後生成的網路也會具有很好的可變性。為了使模型能夠更好地模擬真實世界網路,作者提出了Kronecker圖模型的改進模型,即隨機Kronecker圖模型。在該模型中鄰接矩陣中的元素被替換為機率值,這為Kronecker圖模型帶來了更大的靈活性,使其不僅能夠通過改變參數生成具有一定特性的網路,還可以通過參數估計來模擬真實世界中存在的網路。
