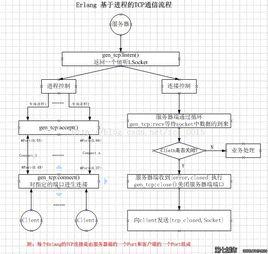
歷史
Erlang得名于丹麥數學家及統計學家Agner Krarup Erlang,同時Erlang還可以表示 Ericsson Language。
Erlang並非一門新語言,它出現於1987年,只是當時對並發、分散式需求還沒有今天這么普遍,當時可謂英雄無用武之地。Erlang語言創始人Joe Armstrong當年在愛立信做電話網路方面的開發,他使用Smalltalk,可惜那個時候Smalltalk太慢,不能滿足電話網路的高性能要求。但Joe實在喜歡Smalltalk,於是定購了一台Tektronix Smalltalk機器。但機器要兩個月時間才到,Joe在等待中百無聊賴,就開始使用Prolog,結果等Tektronix到來的時候,他已經對Prolog更感興趣,Joe當然不滿足於精通Prolog,經過一段時間的試驗,Joe給Prolog加上了並發處理和錯誤恢復,於是Erlang就誕生了。這也是為什麼Erlang的語法和Prolog有不少相似之處,比如它們的List表達都是[Head | Tail]。
1987年Erlang測試版推出,並在用戶實際套用中不斷完善,於1991年向用戶推出第一個版本,帶有了編譯器和圖形接口等更多功能。1992年,Erlang迎來更多用戶,如RACE項目等。同期Erlang被移植到VxWorks、PC和 Macintosh等多種平台,兩個使用Erlang的產品項目也開始啟動。1993愛立信公司內部獨立的組織開始維護和支持Erlang實現和Erlang工具。
特點
Erlang特性:
● 並發性 - Erlang支持超大量級的並發進程,並且不需要作業系統具有並發機制。
● 分散式 - 一個分散式Erlang系統是多個Erlang節點組成的網路(通常每個處理器被作為一個節點)
● 健壯性 - Erlang具有多種基本的錯誤檢測能力,它們能夠用於構建容錯系統。
● 軟實時性- Erlang支持可程式的“軟”實時系統,使用了遞增式垃圾收集技術。
● 熱代碼升級-Erlang允許程式代碼在運行系統中被修改。舊代碼能被逐步淘汰而後被新代碼替換。在此過渡期間,新舊代碼是共存的。
●遞增式代碼裝載-用戶能夠控制代碼如何被裝載的細節。
●外部接口-Erlang進程與外部世界之間的通訊使用和在Erlang進程之間相同的訊息傳送機制。
●Fail-fast(中文譯為速錯),即儘可能快的暴露程式中的錯誤。
●面向並發的編程(COP concurrency-oriented programming)
●函式式編程
●動態類型
●及早求值或嚴格求值
●支持腳本運行
分散式
代碼示例如下:
% create process and call the function web:start_server(Port, MaxConnections)
ServerProcess = spawn (web, start_server, [Port, MaxConnections]),
% create a remote process and call the function web:start_server(Port, MaxConnections) on machine
RemoteNodeRemoteProcess = spawn(RemoteNode, web, start_server, [Port, MaxConnections]),
% send the {pause, 10} message (a tuple with an atom "pause" and a number "10") to ServerProcess (asynchronously)
ServerProcess ! {pause, 10},
% receive messages sent to this process
receive
a_message -> do_something;
{data, DataContent} -> handle(DataContent);
{hello, Text} -> io:format("Got hello message: ~s", [Text]);
{goodbye, Text} -> io:format("Got goodbye message: ~s", [Text])
end.
函式式
Erlang函式大致寫法如下,以一個求整數階乘的模組為例:
 Erlang
Erlang-module(fact). -export([fac/1]).
fac(1) -> 1;
fac(N) when N > 1 -> N * fac(N-1).
註:該檔案要保存成"fact.erl",檔案名稱必須和模組名一致才能編譯通過。
其運行結果如右圖:
下面是快速排序算法的一個Erlang實現:
%% quicksort:qsort(List)
%% Sort a list of items
-module(quicksort).
 Erlang
Erlang-export([qsort/1]).qsort([]) -> [];
qsort([Pivot|Rest]) ->
qsort([ X || X <- Rest, X =< Pivot]) ++ [Pivot] ++ qsort([ Y || Y <- Rest, Y > Pivot]).
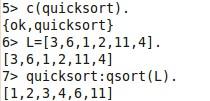
註:該檔案要保存成“quicksort.erl”檔案名稱必須和模組名一致才能編譯通過。其運行結果如右圖。
開發工具
Sublime text
linux下有全套的IDE環境外掛程式可用 完善的如SublimErl ,windows下只能自己簡單的集成一部分基礎功能
優勢比於eclipse 的erlide 是大項目時操作回響速度快 體驗流暢錯誤少
Emacs
可以使用任何你喜歡的編輯器編寫Erlang程式,但如果你使用Emacs編輯可以支持很多功能,比如:代碼縮進、語法高亮、驗證模組名稱、支持段落的注釋、模組骨架、標籤和更多的支持。
有關詳細信息請參閱Erlang Tools 文檔。
Erlide
這是一個基於Eclipse的Erlang圖形界面外掛程式(ErlIDE),ErlIDE正在積極開發新特性,同時它也是開源的。
外掛程式安裝說明
項目連結地址
流量單位
指測量電話呼叫流量的單位。一個厄朗等於一個小時的中繼負荷,或3600秒中繼負荷。如果將CCS(百秒呼叫)轉換成厄朗值,則需先乘以100,然後再除以3600(或直接除以36)。因此,呼叫中心可使用厄朗值來反映中繼線路負荷,即一個小時滿負荷的平均中繼線路有多少數量。例如,在一個小時中,呼叫中心呼叫流量為12.35厄朗時,就意味著在該時段中,平均有12條線多一些都處於全負荷狀態。據此可以大致推算出需要多少座席人員。
指一種數學計算方法,這種方法是基於已知的信息,如平均通話時長,來預測無規則的工作負荷,如電話呼叫量。它是呼叫中心人員和中繼線路數量的決策參考方法。
厄朗公式有兩類,厄朗B用於呼叫量隨機狀態,同時沒有排隊的情況;厄朗C用於呼叫量隨機狀態,同時有排隊的情況,它假設所有來電者將無限期地進入佇列等待被接通。因此,呼叫量不可能比可用的中繼線路數量還大,如果那樣的話,將造成排隊無限期地延遲。
愛爾蘭分布是另一個常用的車頭時距分布,分布的密度函式為:
(15)
式中:k和為參數。對給定參數k,(15)式對應著一種分布,而隨著k取不同的值,可以得到不同的分布函式。因此,愛爾蘭分布適用範圍較廣。特別地,當k=1時,(15)對應著車頭時距為負指數分布的情形,當k=時,(15)對應著車頭時距為均勻分布的情形。研究表明,隨著k 值的增大,說明交通越擁擠,駕駛員行為的隨機程度越小。
對於單條車道上行駛的車輛,車頭時距不能小於最小車頭時距,因此,需要對模型(15)修改,引入帶移位的愛爾蘭分布,分布密度為:
(16)
對於(15)式,有:
(17)
(18)
式中,-樣本均值;S-樣本方差。因此,由(17),(18)兩式可得到參數k和的估計:
(19)
(20)
對於式(16)而言,參數k和仍可分別由(19)和(20)估計,對於參數i由(10)估計。