C4.5算法

C4.5算法是由RossQuinlan開發的用於產生決策樹的算法。該算法是對RossQuinlan之前開發的ID3算法的一個擴展。C4.5算法產生的決策樹可以被用作分類目的，因此該算法也可以用於統計分類。
C4.5算法與ID3算法一樣使用了信息熵的概念，並和ID3一樣通過學習數據來建立決策樹。[1]

一個元組（數據集）本身有很多屬性，怎么知道首先要對哪個屬性進行判斷，接下來要對哪個屬性進行判斷？引入一個概念就是屬性選擇度量。

屬性選擇度量又稱分裂規則，因為它們決定給定節點上的元組如何分裂。屬性選擇度量提供了每個屬性描述給定訓練元組的秩評定，具有最好度量得分的屬性被選作給定元組的分裂屬性。目前比較流行的屬性選擇度量有--信息增益、增益率和Gini指標。

（1）信息增益信息增益實際上是ID3算法中用來進行屬性選擇度量的。它選擇具有最高信息增益的屬性來作為節點N的分裂屬性。該屬性使結果劃分中的元組分類所需信息量最小。對D中的元組分類所需的期望信息為下式：

Info(D)又稱為熵。現在假定按照屬性A劃分D中的元組，且屬性A將D劃分成v個不同的類。在該劃分之後，為了得到準確的分類還需要的信息由下面的式子度量：

信息增益定義為原來的信息需求（即僅基於類比例）與新需求（即對A劃分之後得到的）之間的差，即

（2）信息增益率正是基於此，ID3後面的C4.5採用了信息增益率這樣一個概念。信息增益率使用“分裂信息”值將信息增益規範化。分類信息類似於Info(D)，定義如下：

這個值表示通過將訓練數據集D劃分成對應於屬性A測試的v個輸出的v個劃分產生的信息。信息增益率定義：

選擇具有最大增益率的屬性作為分裂屬性。

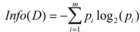
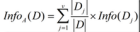
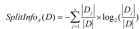
（3）Gini指標Gini指標在CART中使用。Gini指標度量數據劃分或訓練元組集D的不純度，定義為：