基本介紹
Bresenham直線算法是用來描繪由兩點所決定的直線的算法，它會算出一條線段在 n 維光柵上最接近的點。這個算法只會用到較為快速的整數加法、減法和位元移位，常用於繪製電腦畫面中的直線。是計算機圖形學中最先發展出來的算法。
經過少量的延伸之後，原本用來畫直線的算法也可用來畫圓。且同樣可用較簡單的算術運算來完成，避免了計算二次方程式或三角函式，或遞歸地分解為較簡單的步驟。
以上特性使其仍是一種重要的算法，並且用在繪圖儀、繪圖卡中的繪圖晶片，以及各種圖形程式庫。這個算法非常的精簡，使它被實作於各種裝置的固件，以及繪圖晶片的硬體之中。
“Bresenham”至今仍經常作為一整個算法家族的名稱，即使家族中絕大部分算法的實際開發者是其他人。該家族的算法繼承了 Bresenham 的基本方法並加以發展，詳見參考資料。
演算方法
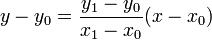Bresenham直線演算法Bresenham直線算法描繪的直線。假設我們需要由 (x0, y0) 這一點，繪畫一直線至右下角的另一點(x1, y1)，x,y分別代表其水平及垂直坐標，並且 x1 - x0 > y1 - y0。在此我們使用電腦系統常用的坐標系，即x坐標值沿x軸向右增長，y坐標值沿y軸向下增長。因此x及y之值分別向右及向下增加，而兩點之水平距離為x1 − x0且垂直距離為y1-y0。由此得之，該線的斜率必定介乎於1至0之間。而此算法之目的，就是找出在x0與x1之間，第x行相對應的第y列，從而得出一像素點，使得該像素點的位置最接近原本的線。
對於由(x0, y0)及(x1, y1)兩點所組成之直線，公式如下：
因此，對於每一點的x，其y的值是
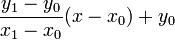Bresenham直線演算法因為x及y皆為整數，但並非每一點x所對應的y皆為整數，故此沒有必要去計算每一點x所對應之y值。反之由於此線之斜率介乎於1至0之間，故此我們只需要找出當x到達那一個數值時，會使y上升1，若x尚未到此值，則y不變。至於如何找出相關的x值，則需依靠斜率。斜率之計算方法為m = (y1 − y0) / (x1 − x0)。由於此值不變，故可於運算前預先計算，減少運算次數。
要實行此算法，我們需計算每一像素點與該線之間的誤差。於上述例子中，誤差應為每一點x中，其相對的像素點之y值與該線實際之y值的差距。每當x的值增加1，誤差的值就會增加m。每當誤差的值超出0.5，線就會比較靠近下一個映像點，因此y的值便會加1，且誤差減1。
下列偽代碼是這算法的簡單表達（其中的plot(x,y)繪畫該點，abs返回的是絕對值）。雖然用了代價較高的浮點運算，但很容易就可以改用整數運算（詳見最佳化一節）：
function line(x0, x1, y0, y1)
int deltax := x1 - x0
int deltay := y1 - y0
real error := 0
real deltaerr := deltay / deltax // 假設 deltax != 0 （非垂直線），
// 注意：需保留除法運算結果的小數部分
int y := y0
for x from x0 to x1
plot(x,y)
error := error + deltaerr
if abs(error) ≥ 0.5 then
y := y + 1
error := error - 1.0
一般化
雖然以上的算法只能繪畫由右上至左下，且斜率小於或等於1的直線，但我們可以擴展此算法，使之可繪畫任何的直線。第一個擴展是繪畫反方向，即由左下至右上的直線。這可以簡單地透過在x0 > x1時交換起點和終點來做到。第二個擴展是繪畫斜率為負的直線。可以檢查y0 ≥ y1是否成立；若該不等式成立，誤差超出0.5時y的值改為加-1。最後，我們還需要擴展該算法，使之可以繪畫斜率絕對值大於1的直線。要做到這點，我們可以利用大斜率直線對直線y=x的反射是一條小斜率直線的事實，在整個計算過程中交換 x 和 y，並一併將plot的參數順序交換。擴展後的偽代碼如下：
function line(x0, x1, y0, y1)
boolean steep := abs(y1 - y0) > abs(x1 - x0)
if steep then
swap(x0, y0)
swap(x1, y1)
if x0 > x1 then
swap(x0, x1)
swap(y0, y1)
int deltax := x1 - x0
int deltay := abs(y1 - y0)
real error := 0
real deltaerr := deltay / deltax
int ystep
int y := y0
if y0 < y1 then ystep := 1 else ystep := -1
for x from x0 to x1
if steep then plot(y,x) else plot(x,y)
error := error + deltaerr
if error ≥ 0.5 then
y := y + ystep
error := error - 1.0
以上的程式可以處理任何的直線，實現了完整的Bresenham直線算法。
最佳化
以上的程式有一個問題：電腦處理浮點運算的速度比較慢，而error與deltaerr的計算是浮點運算。此外，error的值經過多次浮點數加法之後，可能有累積誤差。使用整數運算可令算法更快、更準確。只要將所有以上的分數數值乘以deltax，我們就可以用整數來表示它們。唯一的問題是程式中的常數0.5—我們可以透過改變error的初始方法，以及將error的計算由遞增改為遞減來解決。新的程式如下：
function line(x0, x1, y0, y1)
boolean steep := abs(y1 - y0) > abs(x1 - x0)
if steep then
swap(x0, y0)
swap(x1, y1)
if x0 > x1 then
swap(x0, x1)
swap(y0, y1)
int deltax := x1 - x0
int deltay := abs(y1 - y0)
int error := deltax / 2
int ystep
int y := y0
if y0 < y1 then ystep := 1 else ystep := -1
for x from x0 to x1
if steep then plot(y,x) else plot(x,y)
error := error - deltay
if error < 0 then
y := y + ystep
error := error + deltax
[編輯] 歷史
Jack E. Bresenham於1962年在IBM發明了此算法。據他本人表示，他於1963年在丹佛舉行的美國計算機協會全國大會上發表了該算法，論文則登載於1965年的《IBM系統期刊》 (IBM Systems Journal) 之中。[1]Bresenham直線算法其後被修改為能夠畫圓，修改後的算法有時被稱為“Bresenham畫圓算法”或中點畫圓算法。
