研究背景
 BRS編碼
BRS編碼 BRS編碼
BRS編碼 BRS編碼
BRS編碼 BRS編碼
BRS編碼 BRS編碼
BRS編碼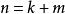 BRS編碼
BRS編碼 BRS編碼
BRS編碼 BRS編碼
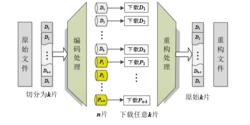
BRS編碼RS編碼是一種在分散式存儲環境下可容錯的編碼方式,它將需要存儲的數據分成 塊,每塊大小為 ,通過編碼矩陣將這 塊數據生成 個編碼塊,其中 ,每個編碼塊存儲在一個存儲節點中,則當編碼塊損失數量不大於 時,系統可以從任意 個編碼塊中修 復所有數據(如右圖所示)。
在傳統RS編碼方式中,使用范特蒙德矩陣作為數據的編碼生成矩陣,將該生成矩陣的逆作為解碼矩陣。傳統RS的編解碼運算都是在一個大的有限域上進行的。
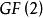 BRS編碼
BRS編碼BRS編碼算法使用的編碼矩陣只包括了數據塊的移位和異或操作,解碼運算使用改進的ZigZag方式解碼。BRS編碼的提出改善了傳統RS編碼性能,因為RS編碼通過在一個大的有限域上運算實現編解碼,BRS編碼將編解碼運算實現在一個大小為 的有限域上,使得編解碼運算都只包含移位和異或操作,提高了編解碼的運算速度。
BRS編碼算法由北京大學先進網路技術實驗室提出,同時發布了BRS編碼的開源實現。在實際環境的測試實驗中,BRS編碼的編解碼速率領先於CRS編碼方式,在分散式存儲系統的設計與實現中,使用BRS編碼存儲方式可以使系統具有再生容錯特性。
編解碼原理
BRS編碼原理
傳統的里德所羅門碼構造都是基於有限域,而BRS碼是基於移位和異或運算的。BRS編碼是基於范德蒙矩陣的,其具體編碼步驟如下:
 BRS編碼
BRS編碼 BRS編碼
BRS編碼1、將原始數據塊平均分成 塊,設每一塊數據塊有 bit數據,記為
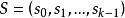 BRS編碼
BRS編碼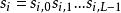 BRS編碼
BRS編碼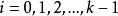 BRS編碼
BRS編碼其中 , 。
 BRS編碼
BRS編碼 BRS編碼
BRS編碼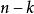 BRS編碼
BRS編碼2、構建檢驗數據塊 , 共有 塊:
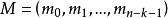 BRS編碼
BRS編碼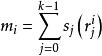 BRS編碼
BRS編碼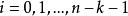 BRS編碼
BRS編碼其中 , 。
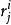 BRS編碼
BRS編碼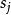 BRS編碼
BRS編碼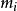 BRS編碼
BRS編碼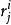 BRS編碼
BRS編碼這裡的加法均為異或操作,其中 表示在原始數據塊 前面添加的“0”的比特數,從而形成校驗數據塊 。 通過如下方式給出:
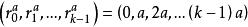 BRS編碼
BRS編碼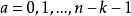 BRS編碼
BRS編碼其中 。
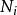 BRS編碼
BRS編碼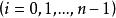 BRS編碼
BRS編碼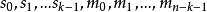 BRS編碼
BRS編碼3、每個結點存儲數據,結點 存儲的數據為 。
BRS編碼示例
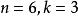 BRS編碼
BRS編碼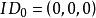 BRS編碼
BRS編碼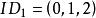 BRS編碼
BRS編碼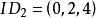 BRS編碼
BRS編碼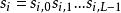 BRS編碼
BRS編碼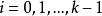 BRS編碼
BRS編碼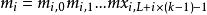 BRS編碼
BRS編碼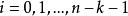 BRS編碼
BRS編碼假如現在, 則有 , , 。每個原始數據塊為 ,其中 ,而每個校驗數據塊為 ,其中 。
校驗數據塊的計算過程如下,加法表示比特位異或運算:
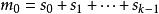 BRS編碼
BRS編碼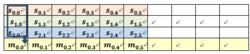 BRS編碼
BRS編碼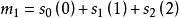 BRS編碼
BRS編碼 BRS編碼
BRS編碼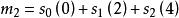 BRS編碼
BRS編碼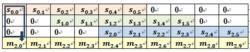 BRS編碼
BRS編碼BRS解碼原理
 BRS編碼
BRS編碼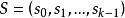 BRS編碼
BRS編碼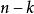 BRS編碼
BRS編碼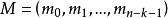 BRS編碼
BRS編碼在BRS碼的構造中我們把原始數據塊平均分成了 塊,有 ,並編碼得到了 塊檢驗數據塊,有 。
在解碼的過程中,有一個必要條件:完好的檢驗數據塊的數目要大於等於損失的原始數據塊的數目,否則無法修復。
以下是解碼的過程分析:
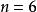 BRS編碼
BRS編碼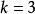 BRS編碼
BRS編碼不妨令 , 。則有
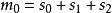 BRS編碼
BRS編碼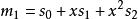 BRS編碼
BRS編碼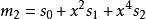 BRS編碼
BRS編碼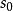 BRS編碼
BRS編碼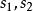 BRS編碼
BRS編碼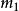 BRS編碼
BRS編碼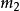 BRS編碼
BRS編碼假設 完好, 缺失,選擇 , 進行修復,令
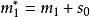 BRS編碼
BRS編碼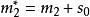 BRS編碼
BRS編碼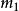 BRS編碼
BRS編碼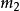 BRS編碼
BRS編碼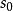 BRS編碼
BRS編碼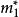 BRS編碼
BRS編碼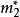 BRS編碼
BRS編碼因為 , , 已知,所以 , 已知。故有:
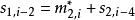 BRS編碼
BRS編碼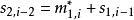 BRS編碼
BRS編碼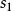 BRS編碼
BRS編碼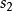 BRS編碼
BRS編碼 BRS編碼
BRS編碼 BRS編碼
BRS編碼根據上面的疊代公式,每循環一次,就能算出2個bit的值( , 中都能得到一個bit)。每個原始數據塊長度為 bit,所以重複 次後,就能解出原始數據塊中的所有未知的bit。以此類推,就完成了數據的解碼。
發表論文
1. H. Hou, K. W. Shum, M. Chen and H. Li, BASIC Regeneration Code: Binary Addition and Shift for Exact Repair, IEEE ISIT 2013 .
2. Jun Chen, Hui Li, Hanxu Hou, Bing Zhu, Tai Zhou, Lijia Lu, Yumeng Zhang, A new Zigzag MDS code with optimal encoding and efficient decoding[C]//Big Data (Big Data), 2014 IEEE International Conference on. IEEE, 2014. .
性能分析
有實驗表明,在編碼速率上,在單核處理器下BRS編碼速率約為RS編碼的600%,約為CRS編碼 的150%,滿足相比RS編碼,編碼速度提升不低於200%。
在同樣條件下,對於不同缺失個數,BRS解碼速率約為RS編碼的400%,約為CRS編碼的130%,滿足相比RS編碼,解碼速度提升100%。
套用範圍
在分散式系統套用日益普及的當前情況下,在分散式存儲系統底層使用糾刪碼存儲數據可以增加系統的容錯性,同時相比於傳統的副本策略,對於相同的冗餘,糾刪碼技術可以成倍地提高系統的可靠性。
BRS編碼可套用在分散式存儲系統中,如在HDFS的使用中,用BRS編碼作為底層數據編碼。由於性能上的優勢和編碼方式上的相似,BRS編碼可以用來替代CRS編碼在分散式系統中的使用。
使用方法
Github上已發布BRS的C語言開源實現,在分散式存儲系統的設計與實現中,可以使用BRS編碼方式存儲數據,實現系統自身的可容錯性。