概述
層次分析法(Analytic Hierarchy Process, AHP)是美國運籌學家、匹茲堡大學T. L. Saaty教授在20世紀70年代初期提出的，AHP是對定性問題進行定量分析的一種簡便、靈活而又實用的多準則決策方法。AHP風險分析法(Analytic Hierarchy Process on Risk Analysis,簡稱)就是將層次分析法用於風險分析的一種定量風險分析方法。
AHPRA的特點
AHP的特點是把複雜問題中的各種因素通過劃分為相互聯繫的有序層次，使之條理化，根據對一定客觀現實的主觀判斷結構把專家意見和分析者的客觀判斷結果直接而有效地結合起來，將一層次元素兩兩比較的重要性進行定量描述。AHPRA利用數學方法計算反映每一層次元素的相對重要性次序的權值，通過所有層次之間的總排序計算所有元素的相對權重並進行排序。
層次分析法自被引入國內以來，以其定性分析定量定量化各種要素的特點，及其靈活簡潔的優點，迅速地在我國風險管理領域得到了廣泛重視和研究。知名項目管理專家郭致星教授在AHPRA這個領域有比較多的研究，並取得了一些成果。
AHPRA的步驟
通過對風險的深刻認識，弄清風險所涉及的範圍、所要採取的措施方案和政策、實現目標的準則、策略和各種約束條件等，廣泛地收集信息。
建立一個多層次的遞階結構，將風險指標分為幾個等級層次。
確定以上遞階結構中相鄰指標指標間相關程度。通過構造兩兩比較判斷矩陣及矩陣運算的數學方法，確定對於上一層次的某個元素而言，本層次中與其相關元素的重要性排序——相對權值。
計算各層指標對風險的合成權重，進行總排序，以確定遞階結構圖中最底層各個指標的總目標中的重要程度。
根據分析計算結果，考慮相應的決策。
1.通過對風險的深刻認識，弄清風險所涉及的範圍、所要採取的措施方案和政策、實現目標的準則、策略和各種約束條件等，廣泛地收集信息。
2.建立一個多層次的遞階結構，將風險指標分為幾個等級層次。
3.確定以上遞階結構中相鄰指標指標間相關程度。通過構造兩兩比較判斷矩陣及矩陣運算的數學方法，確定對於上一層次的某個元素而言，本層次中與其相關元素的重要性排序——相對權值。
4.計算各層指標對風險的合成權重，進行總排序，以確定遞階結構圖中最底層各個指標的總目標中的重要程度。
5.根據分析計算結果，考慮相應的決策。
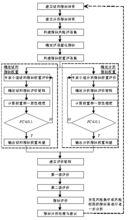AHP風險分析法具體的步驟請參考右圖：
套用實例
可以借用郭致星教授的論文《基於AHP方法的項目研製風險評估》 作為實例，供大家參考。
