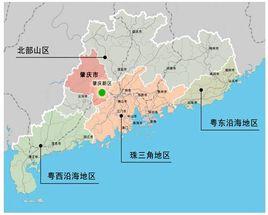
簡介
0-1 規劃是一種特殊形式的整數規劃 。這種規劃的決策變數僅取值 0或1 ,故稱為 0-1 變數或二進制變數 ,因為一個非負整數都可以用二進制記數法用若干個 0-1 變數表示 。 0-1 變數可以數量化地描述諸如開與關、取與棄、有與無等現象所反映的離散變數間的邏輯關係、順序關係以及互斥的約束條件,因此 0-1 規劃非常適合描述和解決如線路設計 、工廠選址 、生產計畫安排、旅行購物、背包問題、人員安排、代碼選取、可靠性等人們所關心的多種問題。
實際上,凡是有界變數的整數規劃都可以轉化為 0-1 規劃來處理 。由於 0-1 規劃具有深刻的背景和廣泛的套用,幾十年來一直受到人們的重視 。0-1 規劃主要用於求解互斥的計畫問題、約束條件互斥問題、固定費用問題和分派問題等方面。
套用
互斥計畫問題
如確定投資項目,選定投資場所,決定投產產品等。設有幾種產品,各產品投產後獲得的利潤為c j,投資限額為 B,規定決策變數 xj的取值為
 圖1
圖1則此0-1規劃的數學模型為
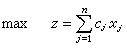 圖2
圖2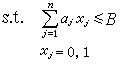 圖3
圖3式中max表示求極大值;s.t.表示“受約束於”; z是目標函式; aj 是各種產品的投資額。
約束條件問題
設有 m個互相排斥的約束條件(≤型) a x+ a x+…+ ax≤ b( i=1,2,…, m),為了保證這 m個約束條件中只有一個起作用,引入 m個 0-1 變數 y 和一個足夠大的常數 M,構造 m+1 個約束條件
a x+ a x+…+ ax≤ b + yM
y+ y+…+ y= m-1
因為 m個 y中只有一個能取 0 值,所以只有一個約束條件能起作用。如運送兩種貨物,其數量分別為 x 和 x,車運時貨物體積不得超過 b ,船運時貨物重量不得超過 b ,即
a x+ a x≤ b(車運),
a x+ a x≤ b(船運)。
若只能採用一種運送方式,這兩個約束條件是互相排斥的。為了統一在一個問題中,引用 0-1 變數 y,設
 圖4
圖4 圖5
圖5把上述約束條件改造成為下面一組約束條件:
a x+ a x≤ b+ y M
a x+ a x≤ b+ yM
y+ y=2-1
式中 M是足夠大的數,採用車運時 y=0 ,由第 1 式即得到車運約束條件,採用船運時 y=0 ,由第 2 式即得到船運約束條件。因此上述互相排斥的約束條件被一組聯立約束條件所代替。
固定費用問題
採用一般線性規劃不能解決固定費用問題,需要用 0-1 規劃。設有 n種生產方式可供選擇, x為採用第 i種方式時的產量, c 為採用第 i種方式時每件產品的變動成本, k為採用第 i種方式時的固定成本,採用各種生產方式的總成本分別為( i=1,2,…, n)
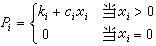 圖6
圖6在構成目標函式時,為了統一在一個問題中討論,引入 0-1 變數 y,即則此0-1規劃的數學模型為
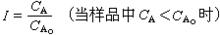 圖7
圖7 圖8
圖8式中min表示求極小值, M是充分大的常數。
分派問題
由幾個人去完成幾項任務,但由於任務性質和各人專長不同,應分派哪個人去完成哪項任務,以使總效率最高或耗費的總時間最小,這類問題稱為分派問題,又稱指派問題。
分派問題必須給出係數矩陣(又稱效率矩陣),矩陣的元素 c(>0)( i,j=1,2,…, n) 表示派第 i人去完成第 j項任務時的效率(或時間、成本等)。引用 0-1 變數 x,設
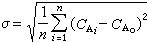 圖9
圖9分派問題的數學模型為
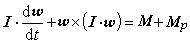 圖10
圖10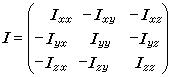 圖11
圖11第 1 個約束條件說明第 j項任務只能由 1人去完成,第 2 個約束條件說明第 i人只能完成 1 項任務。分派問題的解可寫成矩陣形式( x),其各行各列的元素之和都是1。
求解方法
求解 0-1 規劃的方法主要是隱枚舉法(如分枝定界法)。對一些特殊問題還有一些更加有效的方法,例如對指派問題,用D.柯尼希發明的匈牙利法求解更顯方便有效。
0-1 規劃問題一般有三種解法,即變換法、窮舉法和隱枚舉法。變換法用於解特殊的 0-1 規劃問題。窮舉法就是檢查變數取值為 0 或 1 的每一種組合,比較目標函式值來求最優解,這就需要檢查變數取值的 2 個組合。對於 n>10 的情況,這幾乎是辦不到的。因此常設計一些方法,只檢查變數取值組合的一部分,就能得到問題的最優解。這樣的方法稱為隱枚舉法。
採用隱枚舉法解 0-1 規劃問題時要根據目標函式的性質增加一個相應的不等式作為附加約束條件,稱為過濾條件,以減少運算次數。一般還要按目標函式中 x 的係數遞增的順序,重新排列目標函式和約束條件中 x 的次序,以簡化計算。
零一整數規劃
[zero-one integer programming]
0-1 整數規劃是一類最簡單的整數規劃,即變數僅取 0 或 1,
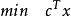 0-1規劃
0-1規劃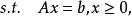 0-1規劃
0-1規劃x 為(1,0)向量
背包問題是一個典型的零一整數規劃。
 0-1規劃
0-1規劃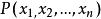 0-1規劃
0-1規劃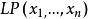 0-1規劃
0-1規劃零一整數規劃可用分枝定界方法來解,方法可簡單敘述如下。設 為 n 個 0-1 整數變數,記原問題為 ,它的鬆弛線性規劃為
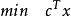 0-1規劃
0-1規劃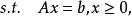 0-1規劃
0-1規劃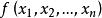 0-1規劃
0-1規劃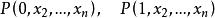 0-1規劃
0-1規劃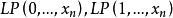 0-1規劃
0-1規劃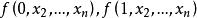 0-1規劃
0-1規劃記其最優解值為 。第一步,解兩個子問題 的鬆弛線性規劃 ,若其最優解值為 ,且兩個解均為整數解,則其中小的一個即為最優解;若其中有一個是整數解且對應最優值小於或等於另一子問題的最優值,則該整數解就是原問題的最優解。以上情形均不滿足時,對最優值較小或小於已有整數解值、且解為非整數的子規划進行對第二個變數的分解。以下步驟的原理是相同的,具體的算法常採用不同的技巧。