龍伯格觀測器

龍伯格（Luenberger）觀測器是由龍伯格與卡爾曼及布西(Bucy)等人所提出的解決動態系統控制率問題的一種防範，建立狀態向量的一個估計值的技術，確定狀態向量的一個適當近似值並把這個值代入理想的控制律。 龍伯格觀測器法適用於其中可用測量結果受噪聲污染不太嚴重的情況，並且產生階數比被觀測系統的階數低的一個動態系統。

龍伯格觀測器的設計

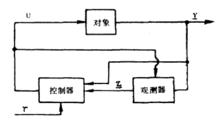觀測器形式

龍伯格觀測器是在反饋通道設定一個補償器，以獲取不可測狀態的信息，系統的一般形式如圖所示。

龍伯格已經證明，對於一個線性定常系統可以用狀態z來建立一個(n-m)階的觀測器，使得z與由Lx給出的系統狀態的一個線性組合相近似，其中L具有(n-m)維．
對於一個線性定常系統的一個(n-m)階觀測器用下式來定義：

z=Dz+Ty+Ru (1.1)

式中D，T，R分別是(n-m)×(n-m)，(n-m)×m和(n-m)×l維的常數矩陣。假設有一個滿足

LA-DL=TC (1.2)
的變換L，並把矩陣月建立為：

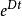龍伯格觀測器

R=LB (1.3)
於是，如果z(0)=Lx(0)，那么當所有t≥0時，z(t)=Lx(t)，或更一般地說，
z(t)=Lx(t)+

(z(0)-Lx(0)) (1.4)
這樣，我們得到
z-Lx=Dz+Ty+Ru-LAx-LBu=Dz+Ty-LAx (1.5)
而根據式(1.2)代替LA，我們得到
z-Lx=D(z-Lx) (1.6)
上式具有式(1.4)作為它的一個解.
如果使觀測器的特徵值比被觀測系統的特徵值負得多，那么觀測器的狀態將收斂於被觀測系統的狀態，收斂之快足以令人滿意地跟蹤被觀測系統的動態特性．
由方程(1.1)定義的觀測器的設計取決於矩陣方程(1.2)的解，使得最後產生的矩陣工具有足夠大的秩，能保證恢復那些不能測量的狀態變數．如果D選擇得使它的特徵值都是相異的，並與A的特徵值不相交，那么式(1.2)具有工的唯一解，
觀測器設計的一種常用計算法是選擇D，然後求出L和T．

龍伯格觀測器的套用

在電液控制系統中的套用

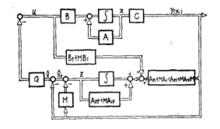帶有觀測器的狀態反饋系統框圖

對電液控制系統進行最優控制,進行極點配置以及其它許多控制形式,都必須採取系統狀態反饋的形式,但是往往得不到系統的所有狀態,因此就要採用狀態估值器來得到狀態的估值,進而實現所要求的控制規律。鑒於電液系統的特點,採用龍伯格觀測器進行降維狀態估值,該裝置已套用在材料試驗機的電液力控制系統中,並得到滿意的結果。

在前饋控制策略中的套用

針對PWM整流器採用前饋控制策略加裝負載電流感測器所產生的問題,產生了一種基於龍伯格觀測器理論的無電流感測器的前饋控制策略,即採用基於龍伯格狀態觀測器的方法取代電流感測器對負載電流進行測量,避免了安裝電流感測器所帶來的增加線路電感、安裝位置困難等問題,尤其當母線掛接多個逆變器負載需要多個感測器時,採用該方法可大大降低成本,提高系統的可靠性。