敘述
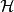黑林格－特普利茨定理
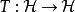黑林格－特普利茨定理
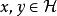黑林格－特普利茨定理設 為希爾伯特空間， 是處處定義的對稱線性運算元，即對任意 都有等式
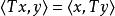黑林格－特普利茨定理。
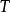黑林格－特普利茨定理那么， 有界（因此也是連續）。
證明
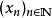黑林格－特普利茨定理
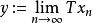黑林格－特普利茨定理
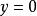黑林格－特普利茨定理 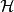黑林格－特普利茨定理從閉圖像定理可知，只需證明：如果序列 趨於0， ，那么 。因為內積在 上連續，故得
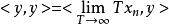黑林格－特普利茨定理
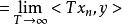黑林格－特普利茨定理
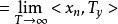黑林格－特普利茨定理 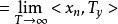黑林格－特普利茨定理
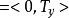黑林格－特普利茨定理=0
所以y=0.
推論
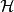黑林格－特普利茨定理1、任何對稱且在 上處處定義的運算元是自伴運算元。
2、無界自伴運算元最多只能定義在希爾伯特空間的一個稠密子集上。
物理結果
這定理帶出了量子力學的數學基礎的一些技術難題。量子力學中的可觀察量對應到某個希爾伯特空間上的自伴算符，但一些可觀察量（如能量）的算符是無界的。這定理說這些算符不能處處定義，只能定義在稠密子集上。
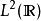黑林格－特普利茨定理
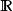黑林格－特普利茨定理
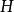黑林格－特普利茨定理
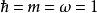黑林格－特普利茨定理以量子諧振子為例。這時希爾伯特空間是 ，即 上平方可積函式空間，能量算符 定義為（設其單位選取使得 ）
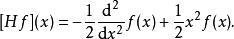黑林格－特普利茨定理 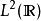黑林格－特普利茨定理這算符是自伴無界的（其特徵值為1/2, 3/2, 5/2, ...），所以不能在整個 上定義。
