基本介紹
 鮑默特-霍爾表
鮑默特-霍爾表 鮑默特-霍爾表
鮑默特-霍爾表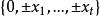 鮑默特-霍爾表
鮑默特-霍爾表定義1設 為正整數, 為t個互相交換的變元,X為元素取自集合 的n×n矩陣,若
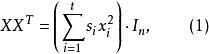 鮑默特-霍爾表
鮑默特-霍爾表 鮑默特-霍爾表
鮑默特-霍爾表 鮑默特-霍爾表
鮑默特-霍爾表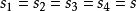 鮑默特-霍爾表
鮑默特-霍爾表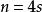 鮑默特-霍爾表
鮑默特-霍爾表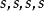 鮑默特-霍爾表
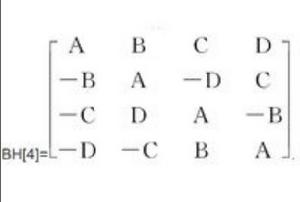
鮑默特-霍爾表則稱X為一個( )-型n階正交設計(orthogonal design)。記作OD(n; )。當t=4, 且 時,OD(4s; )叫做s階 鮑默特-霍爾( Baumert-Hall)陣列或 鮑默特-霍爾(Baumert-Hall)表。1階Baumert-Hall陣列OD(4;1,1,1,1)也叫做Williamson陣列。
鮑默特-霍爾表的構作方法
下面說明Baumert-Hall陣列的構作方法,為此先引入T-序列與循環T-矩陣的概念。
T-序列設
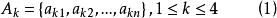 鮑默特-霍爾表
鮑默特-霍爾表是長為n的(0,±1)-序列,若
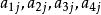 鮑默特-霍爾表
鮑默特-霍爾表(i)對1≤j≤n, 恰有一個為±1,其餘3個均為0,
(ii)對1≤j≤n-1,恆有
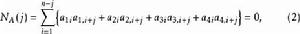 鮑默特-霍爾表
鮑默特-霍爾表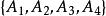 鮑默特-霍爾表
鮑默特-霍爾表則稱 是一組不相交T-序列。簡稱 T-序列(T-sequence)。
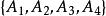 鮑默特-霍爾表
鮑默特-霍爾表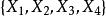 鮑默特-霍爾表
鮑默特-霍爾表循環T-矩陣對上述T-序列 ,設1≤i≤4,令X表示以A為第一行而生成的n階循環矩陣,則稱 為一組n階不相交循環T-矩陣,簡稱 循環T-矩陣。
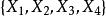 鮑默特-霍爾表
鮑默特-霍爾表引理1設 為n階循環T-矩陣。則
(i)1≤i,j≤4,i≠j,則X與X不相交,即
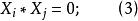 鮑默特-霍爾表
鮑默特-霍爾表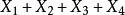 鮑默特-霍爾表
鮑默特-霍爾表(ii) 是一個(1,-1)-矩陣;
(iii)
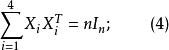 鮑默特-霍爾表
鮑默特-霍爾表(iv)對1≤i≤4,X的各行和都相等,設X的行和為n,則
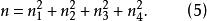 鮑默特-霍爾表
鮑默特-霍爾表下述定理給出構作Baumert-Hall陣列的一個強有力方法。
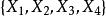 鮑默特-霍爾表
鮑默特-霍爾表定理1(Cooper,J.Wallis) 設 為n階循環T-矩陣,a,b,c,d為交換變元,令
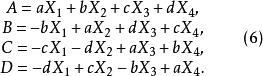 鮑默特-霍爾表
鮑默特-霍爾表再設R為下述n×n矩陣:
 式(7)
式(7)將式(6)與式(7)代入下述Goethal-Seidel陣列
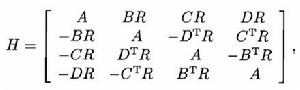 式(8)
式(8)則得到一個OD(4n;n,n,n,n)。
在上述定理中,若取a=b=c=d=1,則得到一個4n階H-陣,於是得到下述結果。
定理2若存在一組長為n的T-序列。則存在4n階H-陣。
定理3若4n≤200,則4n階H-陣存在。