魔群月光猜想

1979年，Con sterousmoon 1992年由Brocherds完成證明。

1979年，Conway和Norton提出了“魔群月光猜想”（monsterousmoonshine）。
存在一個基於魔群的無限維代數結構，通過魔群的不可約線性表示，它恰好給出了j不變數的所有傅立葉係數，而魔群每一個元素在這個代數結構上的作用，都自然地給出了與某個群相關的模形式。

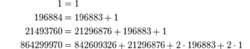
1992年由Brocherds完成證明。證明同時包含了數學和物理，其中用到了弦論中的No-ghost定理來構造證明中必不可少的一個代數結構；1998年Brocherds由於這個證明獲得了菲爾茲獎。通過這個定理架起的橋樑，數學家們也發現了魔群、模函式和弦理論之間更多的千絲萬縷的聯繫，甚至有人過於瘋狂地構想，魔群也許就代表著我們這個宇宙終極的對稱性。