定義和例子
 高階偏導數
高階偏導數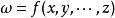 高階偏導數
高階偏導數 高階偏導數
高階偏導數如果定義在開集上的函式的一階偏導數關於某個變數可偏微分,就能作出二階偏導數。同樣能定義階偏導數。我們即將一階以上的偏導數稱為 高階偏導數。將這些高階偏導數記為 :
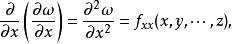 高階偏導數
高階偏導數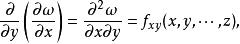 高階偏導數
高階偏導數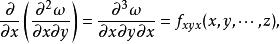 高階偏導數
高階偏導數 高階偏導數
高階偏導數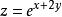 高階偏導數
高階偏導數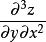 高階偏導數
高階偏導數例 1 求函式的所有二階偏導數和.
解 由於函式的一階偏導數是
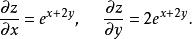 高階偏導數
高階偏導數因此有
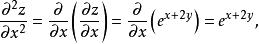 高階偏導數
高階偏導數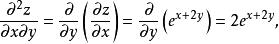 高階偏導數
高階偏導數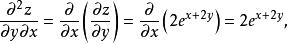 高階偏導數
高階偏導數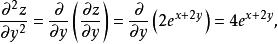 高階偏導數
高階偏導數和
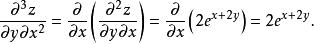 高階偏導數
高階偏導數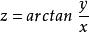 高階偏導數
高階偏導數例2 求函式的所有二階偏導數。
解 因為
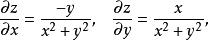 高階偏導數
高階偏導數所以二階偏導數為
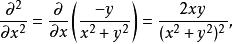 高階偏導數
高階偏導數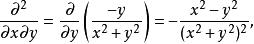 高階偏導數
高階偏導數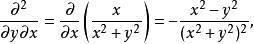 高階偏導數
高階偏導數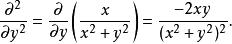 高階偏導數
高階偏導數高階偏導數和求導順序無關的條件
 高階偏導數
高階偏導數 高階偏導數
高階偏導數 高階偏導數
高階偏導數 高階偏導數
高階偏導數從上面兩個例子可以看到,這些函式關於和的不同順序的兩個二階偏導數都相等(這種既有關於又有關於的高階偏導數稱為 混合偏導數),即
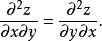 高階偏導數
高階偏導數但這個結論並不對任何函式都成立,例如函式
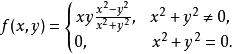 高階偏導數
高階偏導數它的一階偏導數為
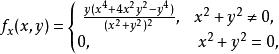 高階偏導數
高階偏導數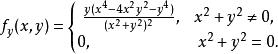 高階偏導數
高階偏導數 高階偏導數
高階偏導數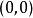 高階偏導數
高階偏導數 高階偏導數
高階偏導數 高階偏導數
高階偏導數進而求在處關於和的兩個不同順序的混合偏導數,得
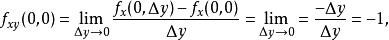 高階偏導數
高階偏導數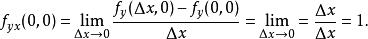 高階偏導數
高階偏導數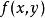 高階偏導數
高階偏導數由此看到,這裡的在原點處的兩個二階偏導數與求導順序有關。那么,在什麼條件下混合偏導數與求導順序無關呢?
定理
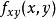 高階偏導數
高階偏導數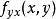 高階偏導數
高階偏導數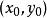 高階偏導數
高階偏導數若和都在點連續,則
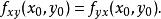 高階偏導數
高階偏導數 高階偏導數
高階偏導數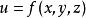 高階偏導數
高階偏導數這個定理的結論對元函式的混合偏導數也成立。如三元函式,若下述六個三階混合偏導數
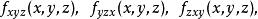 高階偏導數
高階偏導數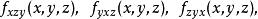 高階偏導數
高階偏導數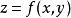 高階偏導數
高階偏導數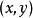 高階偏導數
高階偏導數 高階偏導數
高階偏導數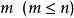 高階偏導數
高階偏導數在某一點連續,則在這一點六個混合偏導數都相等。同樣,若二元函式在點存在直到階的連續混合偏導數,則在這一點階混合偏導數都與順序無關 。
複合函式的高階偏導數
 高階偏導數
高階偏導數 高階偏導數
高階偏導數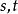 高階偏導數
高階偏導數設是通過中間變數而成為的函式,即
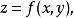 高階偏導數
高階偏導數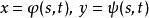 高階偏導數
高階偏導數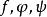 高階偏導數
高階偏導數 高階偏導數
高階偏導數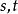 高階偏導數
高階偏導數其中。若函式都具有連續的二階偏導數,則作為複合函式的對同樣存在二階連續偏導數。具體計算如下:
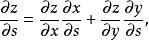 高階偏導數
高階偏導數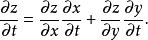 高階偏導數
高階偏導數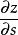 高階偏導數
高階偏導數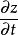 高階偏導數
高階偏導數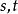 高階偏導數
高階偏導數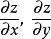 高階偏導數
高階偏導數 高階偏導數
高階偏導數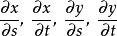 高階偏導數
高階偏導數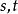 高階偏導數
高階偏導數 高階偏導數
高階偏導數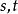 高階偏導數
高階偏導數顯然與仍是的複合函式,其中是的函式,是的函式。繼續求關於的二階偏導數
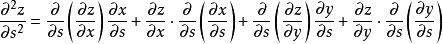 高階偏導數
高階偏導數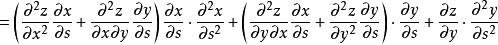 高階偏導數
高階偏導數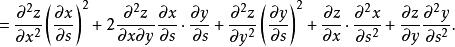 高階偏導數
高階偏導數同理,我們可以計算另外兩個二階偏導數 。
