介紹
高斯-勒讓德算法是一種用於計算π的算法。它以迅速收斂著稱,只需25次疊代即可產生π的4500萬位正確數字。不過,它的缺點是記憶體密集,因此有時它不如梅欽類公式使用廣泛。
該方法基於卡爾·弗里德里希·高斯(1777–1855)和阿德里安-馬里·勒讓德(1752–1833)的個人成果與乘法和平方根運算的現代算法的結合。該算法反覆替換兩個數值的算術平均數和幾何平均數,以接近它們的算術-幾何平均數。
下文的版本也被稱為 高斯-歐拉,布倫特-薩拉明(或薩拉明-布倫特)算法;它於1975年被理察·布倫特和尤金·薩拉明獨立發現。日本筑波大學於2009年8月17日宣布利用此算法計算出π小數點後2,576,980,370,000位數字,計算結果用波溫算法檢驗。
知名的計算機性能測試程式Super PI也使用此算法。
算法
設定初始值:
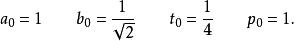 高斯-勒讓德算法
高斯-勒讓德算法 高斯-勒讓德算法
高斯-勒讓德算法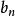 高斯-勒讓德算法
高斯-勒讓德算法反覆執行以下步驟直到 與 之間的誤差到達所需精度:
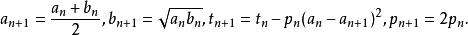 高斯-勒讓德算法
高斯-勒讓德算法則π的近似值為:
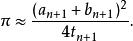 高斯-勒讓德算法
高斯-勒讓德算法下面給出前三個疊代結果(近似值精確到第一個錯誤的位數):
3.140...
3.14159264...
3.1415926535897932382...
該算法具有二階收斂性,本質上說就是算法每執行一步正確位數就會加倍。
數學背景
算術-幾何平均數的極限
a和b兩個數的算術-幾何平均數,是通過計算它們的序列極限得到的:
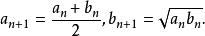 高斯-勒讓德算法
高斯-勒讓德算法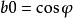 高斯-勒讓德算法
高斯-勒讓德算法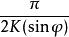 高斯-勒讓德算法
高斯-勒讓德算法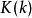 高斯-勒讓德算法
高斯-勒讓德算法兩者匯聚於同一極限。
若 a=1且
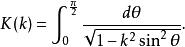 高斯-勒讓德算法
高斯-勒讓德算法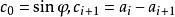 高斯-勒讓德算法
高斯-勒讓德算法若,則
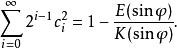 高斯-勒讓德算法
高斯-勒讓德算法其中E(k)為第二類完全橢圓積分:
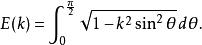 高斯-勒讓德算法
高斯-勒讓德算法高斯知道以上這兩個結果。
勒讓德恆等式
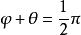 高斯-勒讓德算法
高斯-勒讓德算法 高斯-勒讓德算法
高斯-勒讓德算法 高斯-勒讓德算法
高斯-勒讓德算法對於滿足的與,勒讓德證明了以下恆等式:
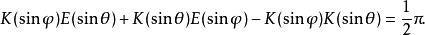 高斯-勒讓德算法
高斯-勒讓德算法高斯-歐拉法
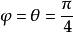 高斯-勒讓德算法
高斯-勒讓德算法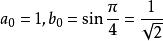 高斯-勒讓德算法
高斯-勒讓德算法的值可以代入勒讓德恆等式,且K、E的近似值可通過的算術-幾何平均數的序列項得到。
