歷史
馬呂斯定理是法國物理學家艾蒂安-路易·馬呂斯在1808年闡述的一條幾何光學的定理。
內容
在均勻介質中的光線束，如果有一個共點，例如從同一個點光源發射，這樣的光束稱為同心光束。同心光束有正交一致性，即光束中所有的一切光線，都和以同源點為中心的一切球面正交。根據光在均勻介質中傳播的性質，這些球面無非是光波動光前，光線自然和波前正交。
馬呂斯定理：“正交一致性光束，經過無論多少次的反射和折射，始終保持正交一致”。
證明
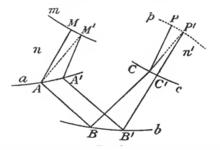圖1.馬呂斯定理的證明1889年瑞利男爵在《大英百科全書》第九版《光學》條中，給出根據費馬原理的證明。
設同源光束[MABCP]與[M'A'B'C'P']與曲面m分別在M,M'點正交；這兩道光線在傳播過程中經過多次反射或折射，分別與界面a相交於A，A'點；與界面b相交於B,B'點，與界面c 相交於C,C'點；經過若干反射、折射後分別到達P，P'點；令光線[MABCP]、[M'A'B'C'P'] 的光程相等；則所有等光程的P,P'的集合，形成一個曲面p。可證明光線[MABCP]與曲面p在P點正交，光線[M'A'B'C'P']與曲面p在P'點正交，即集合p是光束的正交一致性曲面。
證：
作兩條附加直線M'A和P'C。令M與M'無限接近，因M'A與曲面m 垂直，光線[M'ABCP']與光線[M'A'B'C'P']之差是MM'線段的高次微小項
即[M'ABCP']～[M'A'B'C'P']。但根據費馬原理的要求，[M'A'B'C'P]=[MABCP]，代入前式，可得
[M'ABCP']=[MABCP];
令第一介質和最後介質的折射率分別為n,n'，則消除共同線段之後可得：
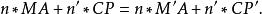馬呂斯定理由此
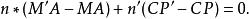馬呂斯定理在M和M'無限接近時M'A=MA，於是 CP'=CP;即CP,CP'是等腰三角形的兩腰，與PP'夾角相等；當其無限接近時CP,CP'合為一體，垂直於曲面p。同理可證C'P'垂直於p。
