定義
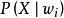類條件機率密度
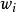類條件機率密度
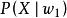類條件機率密度
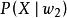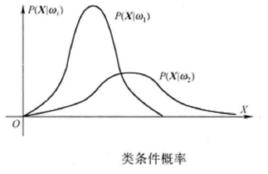
類條件機率密度類條件機率密度函式 是指在已知某類別的特徵空間中，出現特徵值X的機率密度，指第 類樣品其屬性X是如何分布的。假定只用其一個特徵進行分類，即n=1，並已知這兩類的類條件機率密度函式分布，如圖1所示，機率密度函式 是正常藥品的屬性分布，機率密度函式 是異常藥品的屬性分布。
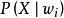類條件機率密度 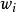類條件機率密度 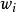類條件機率密度例如，全世界華人占地球上人口總數的20%，但各個國家華人所占當地人口比例是不同的，類條件機率密度函式 是指 條件下出現X的機率密度，在這裡指第 類樣品其屬性X是如何分布的。
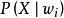類條件機率密度在工程上的許多問題中，統計數據往往滿足常態分配規律。常態分配簡單、分析方便、參量少，是一種適宜的數學模型。如果採用正態密度函式作為類條件機率密度的函式形式，則函式內的參數，如期望和方差是未知的。那么問題就變成了如何利用大量樣品對這些參數進行估計，只要估計出這些參數，類條件機率密度函式 也就確定了。
在大多數情況下，類條件密度可以採用多維變數的正態密度函式來模擬。
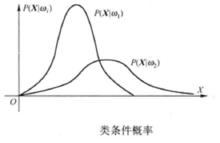圖1相關概念
貝葉斯公式
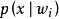類條件機率密度
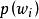類條件機率密度貝葉斯分類器依據類條件機率密度 和先驗機率 來判別樣本工的類別屬性，因此在構建分類器時需要估計出每個類別的先驗機率，並且確定類條件機率密度。作為類條件機率密度的“機率模型”可以有很多種形式，這需要根據解決的具體問題來確定。高斯分布由於其形式簡單、易於分析，並且在很多實際套用中能夠取得較好的識別效果，因此常常被用來作為貝葉斯分類器的機率模型。
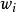類條件機率密度 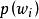類條件機率密度 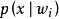類條件機率密度若已知總共有M類物體，以及各類在這n維特徵空間的統計分布，具體來說是已知各類別 ，i=1，2，…，M的先驗機率 及類條件機率密度函式 。對於待測樣品，貝葉斯公式可以計算出該樣品分屬各類別的機率，叫做後驗機率；看X屬於那個類的可能性最大，就把X歸於可能性最大的那個類，後驗機率作為識別對象歸屬的依據。貝葉斯公式為
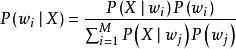類條件機率密度類別的狀態是一個隨機變數．而某種狀態出現的機率是可以估計的。貝葉斯公式體現了先驗機率、類條件機率密度函式、後驗機率三者關係的式子。
先驗機率
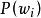類條件機率密度 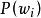類條件機率密度先驗機率 針對M個事件出現的可能性而言，不考慮其他任何條件。
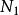類條件機率密度
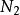類條件機率密度例如，由統計資料表明總藥品數為N，其中正常藥品數為 ，異常藥品數為 ，則
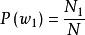類條件機率密度
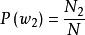類條件機率密度
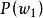類條件機率密度
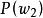類條件機率密度 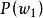類條件機率密度 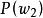類條件機率密度我們稱 及 為先驗機率。顯然在一般情況下正常藥品占比例大，即 > ：僅按先驗機率來決策，就會把所有藥品都劃歸為正常藥品，並沒有達到將正常藥品與異常藥品區分開的目的。這表明由先驗機率所提供的信息太少。
相關概念的區別
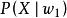類條件機率密度 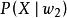類條件機率密度
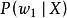類條件機率密度
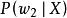類條件機率密度、 、 、 的區別
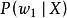類條件機率密度 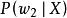類條件機率密度
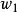類條件機率密度
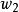類條件機率密度 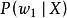類條件機率密度 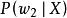類條件機率密度① 和 是在同一條件X下， 與 出現的慨率，若 > ，
則可以得到：在條件 X下，事件 出現的可能性比事件 大。
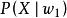類條件機率密度 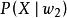類條件機率密度 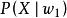類條件機率密度 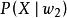類條件機率密度 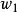類條件機率密度 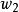類條件機率密度 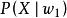類條件機率密度 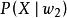類條件機率密度 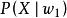類條件機率密度 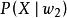類條件機率密度 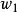類條件機率密度 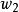類條件機率密度② 與 都是指各自條件下出現X的可能性，兩者之間沒有聯繫，比較兩者沒有意義。 和 是在不同條件下討論的問題，即使只有兩類 與 ， + ≠1。不能僅因為 大於 ，就認為X是第一類事物的可能性較大。只有考慮先驗機率這一因素，才能決定X條件下，判為 類或 類的可能性比較大。
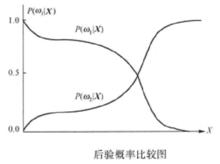圖2