回歸分析法
所謂回歸分析法,是在掌握大量觀察數據的基礎上,利用數理統計方法建立因變數與自變數之間的回歸關係函式表達式(稱回歸方程式)。回歸分析中,當研究的因果關係只涉及因變數和一個自變數時,叫做一元回歸分析;當研究的因果關係涉及因變數和兩個或兩個以上自變數時,叫做多元回歸分析。此外,回歸分析中,又依據描述自變數與因變數之間因果關係的函式表達式是線性的還是非線性的,分為線性回歸分析和非線性回歸分析。通常線性回歸分析法是最基本的分析方法,遇到非線性回歸問題可以藉助數學手段化為線性回歸問題處理。
非線性回歸簡介
如果回歸模型的因變數是自變數的一次以上函式形式,回歸規律在圖形上表現為形態各異的各種曲線,稱為非線性回歸。 這類模型稱為非線性回歸模型。在許多實際問題中,回歸函式往往是較複雜的非線性函式。非線性函式的求解一般可分為將非線性變換成線性和不能變換成線性兩大類。
處理方法
可線性化問題
處理可線性化處理的非線性回歸的基本方法是,通過變數變換,將非線性回歸化為線性回歸,然後用線性回歸方法處理。假定根據理論或經驗,已獲得輸出變數與輸入變數之間的非線性表達式,但表達式的係數是未知的,要根據輸入輸出的n次觀察結果來確定係數的值。按最小二乘法原理來求出係數值,所得到的模型為非線性回歸模型(nonlinear regression model)。
不可線性化問題
 非線性回歸
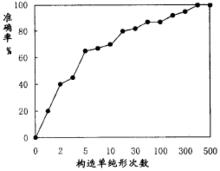
非線性回歸對實際科學研究中常遇到不可線性處理的非線性回歸問題,提出了一種新的解決方法。該方法是基於回歸問題的最小二乘法,在求誤差平方和最小的極值問題上,套用了最最佳化方法中對無約束極值問題的一種數學解法——單純形法。套用結果證明,這種非線性回歸的方法算法比較簡單,收斂效果和收斂速度都比較理想。
 非線性回歸
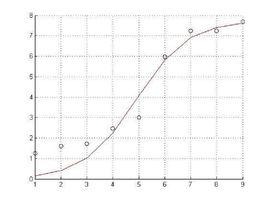
非線性回歸在熟練掌握最小二乘法的情況下,解決上述問題的關鍵是確定曲線類型和怎樣將其轉化為線性模型。確定曲線類型一般從兩個方面考慮:一是根據專業知識,從理論上推導或憑經驗推測、二是在專業知識無能為力的情況下,通過繪製和觀測散點圖確定曲線大體類型。
非線性回歸例題
例1:1790-1960某國人口變化數據:注意:即便線性方程對對觀測數據擬合相當好,但有關誤差項的獨立性和方差假設有可能被破壞。原因是時間序列的數據誤差項往往不獨立,誤差項大小有可能根據數據總體的大小而變化,意思就是,即便適合這個樣本的觀測量的方程,但是,不適合總體。根據經驗,人口增長模型不能被轉化為線性模型,所以,可以利用曲線回歸或者非線性回歸。進一步比較究竟是曲線回歸好還是非線性回歸好,需要建立新的殘差變數,這一步並不難,就是在spss中,相應分析的保存子對話框中建立新的對應模型的變數。其實,有一個萬能公式:spss中,所有的“保存”對話框的功能都是,在二維表視窗也就是spss的盛放數據視窗中建立新變數,這個新變數有默認名,是相應分析的重要結果。保存新變數以後,需要根據殘差的序列圖進行判斷:最平穩的就是最合適的。
例2:血中藥物濃度和時間曲線呈非線性關係。
這個是根據專業背景知識而判斷。藥物不可能馬上見效,也許在血液中逐步或者突然見效。
例3:身高和體重,在青少年中,是呈直線關係,因為,青少年在不斷成長,但是,對於整個人的生命周期,確是曲線關係 因為,成年人的身高一般是確定的。
像這樣的例子根本用直線回歸擬合不了,也稱為非本質線性模型。對於這種實際情況,可以使用非線性回歸的分段模型。最終目的是使殘差平方和最小。也就是在圖形中跟大多數散點接近。
利用SPSS做非線性回歸
注意事項
1 初始值確定:
①利用簡單假設確定,例如,如果在所有變數中最大的一個個案值為178萬,就需要選擇200為初始值,再根據方程估計參數值。
②利用圖形或者圖形輔助,數據轉換
如果參數沒有初始值,也不能簡單的設定為0,要將它們設定為預計要改變的值大小。總之,就是想辦法找到一個比較合適的值,多設幾個,然後比較。也可以根據專業背景和重點,來設值。這個還可以根據數學計算,例如,方程二邊同時取對數。需要具體問題具體分析。
2 疊代和收斂:疊代是計算機自動計算的,例如將疊代設定為1000,意思就是計算機算了1000次,每一次都是根據上一次的結果的基礎進行再運算。當然,人工筆算需要算1000年。疊代不會永無止境的計算下去,而是收斂標準或者稱作最大疊代的設定後,不論得沒有得到結果,是否達到目標,都會停止。在結果輸出表格中有疊代的歷史記錄。這個表格就是過程表,每一步怎樣算的,都可以找到。因為疊代是計算機自動計算,例如,燒水,如果開了不斷電,水燒乾了就會起火,所以,機器需要人控制,它本身沒有情感。
spss操作:不論“計算變數”對話框或者“非線性回歸”,和非線性回歸的“損失函式”對話框都是很像的,有一個計算器算盤,函式組,函式和特殊變數。各種元素組合在一起,構成一個表達式,這個表達式構成一個新變數。只要用滑鼠將對應的元素加入到表達式中,然後檢查,或者事先在本上寫有表達式,對應好,基本就沒有問題。其實,spss許多操作根據文字可以猜出個大概。
3 損失函式:“非線性回歸”對話框是對整個因變數的運算法則,但是,損失函式是對某一個統計量的運算法則,spss默認是使用最小殘差平方和找出非線性模型,也可以自己設定。在相應對話框中都有設定。可以這樣以為:損失函式就是估計誤差的函式,它是一個負面指標,越小越好。
4 參數約束:多數非線性模型中,參數必須限制在有意義的區間內。指的是在疊代過程中對參數的限制。分為線性約束和非線性約束。線性約束中將參數乘以常數 但這個常數不能為其他參數或者自身。非線性約束中至少有一個參數和其他參數相乘或者相除或者進行冪運算。
結果比較
1 估計參數的漸進相關矩陣:如果出現非常大的正值或者負值,可能因為模型中參數過多,也說明觀測量數目不足,但是不說明模型不擬合。
2 95%置信區間:如果95%置信區間不包括零,表明這個參數具有統計學意義。如果離零比較接近,下結論時候應慎重。
3 曲線擬合中計算出來的決定係數實際上是曲線直線化直線方程的決定係數,不一定代表變換前的變異解釋程度。也就是說二個模型的決定係數有可能不具有可比性。