概述
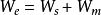靜電能對於一個帶電體系的靜電能，應包括每個帶電體的自能和帶電體問相互作用能。所謂“自能”就是將一個帶電體看成無窮個帶電微元，將這些無窮多個帶電體微元從無限分散狀態聚集成該帶電體，外力所做功的大小。所謂“互能”則是將帶電體系統中，各帶電體從現在位置彼此分開至無窮遠時，它們之問的靜電力所做的功。
靜電能包括自能和互能.點電荷的自能是無窮大，一般在靜電學問題中都不考慮點電荷的自能。
點電荷系
由一電場和一個被搬運電荷構成的體系的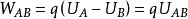靜電能
靜電能電場力搬運電荷做功提升或消耗了體系的勢能。在電場中搬運一個正電荷的過程中，無論電場力做
正功還是負功，都表明了電場具有能的屬性。電場力做正功則降低了體系的勢能，做負功則提升了體系
的勢能，若用W 表示電場力做功，則電場力對電荷的做功可由下式計量
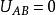靜電能
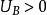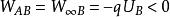靜電能
靜電能若 A 點取在無限遠處，即 ，若 ，則 ，負號表示“電場力做負功，也就是外力克服電場力做正功”。這一份功對於電荷與電場這個體系的能量是建設性的，具有提升其勢能的作用，就如同我們將一個重物提升高度而提升了重力勢能一樣。
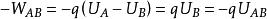靜電能由上所述不難理解，電場力做功與體系的電勢能完全遵守“功能原理”而互相轉化，若用外W 表示外力做功，其轉換關係就是 即外力做功積累或提升了體系的電勢能。上述討論的目的是要搞清楚“外力做功”、“電場力做功”及“電勢能”三者之間的關係，明白了三者之間的關係自然就能理解“外力對搬運電荷做功提升或消耗了帶電體系的靜電能”這個道理。
兩個相距為r 的點電荷q1、q2 構成的系統的靜電能
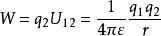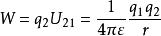靜電能
靜電能一個真空中的電荷系統可以看作是由若干彼此相距無限遠的點電荷匯聚到一起形成的。兩個點電荷的系統亦如此，可以看作從無限遠處把q1 搬運到P 點，把q2 搬運到 Q 點，這一過程可以是先搬運q1 後搬運 q2，也可以是先搬運q2 後搬運q1。顯然搬運第一個電荷對系統的靜電能無貢獻，搬運第二個電荷就需要外界對第二個電荷做正功或第一個電荷的電場對第二個電荷做負功，注意相互作用的做功量度為 或
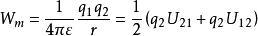靜電能由於這類做功改變了體系的靜電能，屬於兩個電荷之間相互作用能的變化，因而又可以用體系的相互作用能來表示，即 這一相互作用能的積累顯然是由外力做功或第一個電荷的電場力做負功轉變而來的，故這也是體系靜電能的另一個稱呼。
孤立帶電體
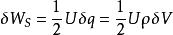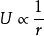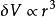靜電能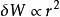
靜電能
靜電能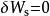
靜電能
靜電能任何帶電體的電荷都可以看成是由原來無限分散的許多電荷元緩慢地匯聚起來的，所以其總靜電能應等於諸電荷元的自能和電荷元之間的互能之和。先討論一下電荷元的自能，設電荷元的電量為，其能量為 一般ρ 可以認為常量，而 ， ，所以 當電荷元取得足夠小時，r →0， ，說明電荷元的自能為零。可見，帶電體的靜電能是組成該帶電體的電荷元之間的互能的總合。當然，也可將其視為帶電體的自能。
帶電體系
設空間某一區域，有一電荷任意分布的帶電體系（由有限個帶電體組成），其穩定的最終狀態的電荷體密度為ρ（x,y,z），電荷面密度為σ（x,y,z），電勢為U(x,y,z)。因為靜電場是保守力場，所以系統的總能量取決於系統的最終狀態，而與系統形成的過程無關。故構想：每一個帶電體的電量都同時從零開始，按同一比例k 緩慢地增加到最終值，設初值為0，終值為1，根據場的疊加原理，空間各點的電勢亦按同一比值k 增加，即kU(x,y,z)
