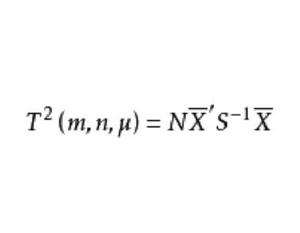基本概念
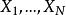霍特林統計量
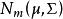霍特林統計量
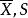霍特林統計量 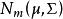霍特林統計量設 是獨立的 隨機向量， 分別為來自 的樣本均值與樣本協差陣，則有以下定義。
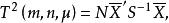霍特林統計量定義1
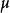霍特林統計量 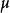霍特林統計量稱為Hotelling的T統計量，m，n為自由度， 為總體均值,當 =0時，T統計量常簡記為T(m，n)，它的分布稱為T分布，記作：T～T(m，n)。
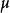霍特林統計量 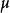霍特林統計量
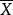霍特林統計量 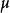霍特林統計量T統計量是Hotelling於1931年首先提出的，它是一元統計分析中t統計量在多元分析中的直接推廣，因為當m=1時，T²就是通常用來檢驗是否均值 =0的t統計量的平方。一般情況下。顯然T²≥0，且如果 =0。則 應該接近0，於是T²也應接近0，因此，如果T²的觀測值足夠大，則可認為有理由拒 絕零假設H： =0。在一元統計分析中，t分布已有專門的t分布表可查，對於t分布在多元統計分析中的推廣的T²分布也有專門的T²(m，n)分布表可查。
相關結論
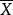霍特林統計量 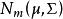霍特林統計量
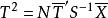霍特林統計量定理1 設 與S為來自 的容量為N=n+1的樣本均值與樣本協差陣，(其中n≥m)，令 ，則
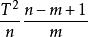霍特林統計量
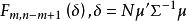霍特林統計量
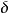霍特林統計量 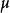霍特林統計量 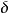霍特林統計量
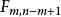霍特林統計量為 ，即具有自由度m與n-m+1的參數為 的非中心F分布。當 =0時，則 =0，這時就成為中心F分布 。
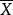霍特林統計量 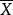霍特林統計量
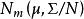霍特林統計量
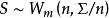霍特林統計量證明 因為 與S相互獨立， 為 ，且 ，於是
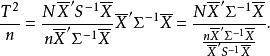霍特林統計量由相關定理知
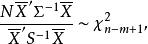霍特林統計量 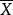霍特林統計量 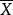霍特林統計量 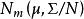霍特林統計量且與 相互獨立。又因 ～ ， 由相關定理知，
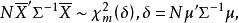霍特林統計量因此
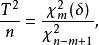霍特林統計量其中分子與分母是相互獨立的，將分子分母分別用它們對應的自由度除之，並根據非中心F分布定義，有
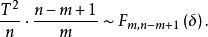霍特林統計量證畢。
這個定理的最大優點是它 把T統計量化成為F分布。
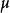霍特林統計量 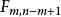霍特林統計量這裡關於T分布的推導是由Wijsman 1957年給出的。注意，當 =0時，T簡記作T(m，n)，此時(n一m+1)T/nm的分布為中心 分布。
因此，檢驗
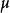霍特林統計量 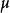霍特林統計量零假設H： =0；備擇假設H： ≠0時，在水平α下，如果
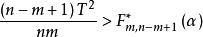霍特林統計量
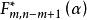霍特林統計量 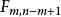霍特林統計量則拒絕H，接受H。其中 表示 分布的上100α%位點。
