引入與定義
在電場中存在電介質的情況下,
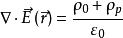 電位移矢量
電位移矢量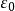 電位移矢量
電位移矢量電場強度等於自由電荷和極化電荷所激發的場的疊加, 為真空中的介電常數,移項得:
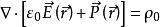 電位移矢量
電位移矢量方括弧中項只與電荷密度有關,因此將括弧中項稱為電位移矢量,即:
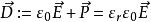 電位移矢量
電位移矢量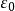 電位移矢量
電位移矢量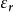 電位移矢量
電位移矢量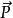 電位移矢量
電位移矢量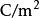 電位移矢量
電位移矢量( 為真空介電常數 , 為此電介質的相對介電常數; 為電極化強度;國際單位制(SI)中 單位: )
積分形式
高斯定理
對於空間中任意的閉合曲面S及其圍住的體積V,都有:
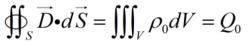 電位移矢量
電位移矢量Q0是被閉合曲面S包住的自由電荷總量。
微分形式
麥克斯韋方程組
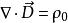 電位移矢量
電位移矢量微分形式 :
即電位移矢量的散度等於該點電荷密度。
這式子的好處是它在形式上與極化電荷無關 ,簡化了對問題的討論。
套用
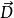 電位移矢量
電位移矢量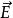 電位移矢量
電位移矢量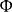 電位移矢量
電位移矢量有介質時,可以直接通過自由電荷的分布求出 ,並進而求得 與 。
電位移矢量與做功的比較
D=εE W=Fs
位移電流和電位移矢量的關係
電位移矢量是一個用以描述電場的輔助物理量,是矢量。因為物質有極化作用,是真空中的高斯定律修正。
位移電流是電位移矢量時間變化率的量,並對面積分。因為這個量同電流一樣產生磁場,故稱為位移電流,但本質並非電流,而是電場變化率。所以磁場的產生除了電荷運動外,還有電場的變化。

