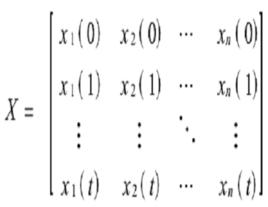基本概念
離散系統
早在五十年代，由於數字計算機在工程和科學上套用的增加，離散控制系統的研究己經引起了人們的注意，當時的工作主要是套用z變換研究採樣數據系統。近三十年來，離散控制系統的研究已經有了較大的發展。尤其是近幾十年來，隨著科學技術的高速發展，人類社會進入到信息化，工業技術發生了根本性變革，出現了一大批高新技術領域世界範圍的微電子技術革命浪潮，極大地推動了微處理機和微型計算機在控制系統種的套用。由於數字計算機進行計算機時在時間上是離散的，因此當一個系統用數字計算機進行控制或用數字計算機模擬、分析、設計控制系統時，需要把時間變數考慮為離散變數，研究的系統需要考慮為離散系統，由於這些原因，近來離散控制系統的研究再次引起了控制界的特別重視，目前離散控制系統的分析與設計已成為控制理論的一個重要組成部分。
隨著微型機的多功能性及可靠性的不斷提高，加之其價格的日益下降，套用微型計算機進行控制和管理日益廣泛。例如用小型機代替二次儀表對生產過程進行控制時，其不僅可以實現PID控制，還可以實現一些複雜控制。更進一步，還可以套用離散控制系統的理論和方法，設計更高級的反饋系統，以達到諸如最優控制、線性多變數控制、自適應控制等等。又如用微機對一個工廠、一個公司以至一個比較複雜的管理系統管理時，通過建立數學模型，利用離散系統的理論和方法進行分析與設計，可以得到令人滿意的管理策略。由於數字計算機處理的只能時離散的數位訊號，所以，不論它用於控制或用於管理，如果原來的信號時連續的，都需要將它離散化，轉換成離散信號。這就是說，需要通過離散化把原來的連續控制系統轉換成一個離散控制系統來處理。因此研究離散系統具有重要的現實意義。
動態系統
動態系統是指系統狀態隨時間而變化的系統或者按確定性規律隨時間演化的系統。
按確定性規律隨時間演化的系統，又稱動力學系統。動態系統理論來源於經典力學。美國數學家G.D.伯克霍夫發展了法國數學家H.龐加萊在天體力學和微分方程定性理論方面的研究，奠定了動力學系統理論的基礎。動態系統的首要特徵就是該系統由多種變數或參數構成，這些變數相互聯繫，並處在恆動之中。動態系統可以是城市的交通系統或森林的生態系統，也可以是一個言語社區。同時，二語學習者自身可視為一個動態系統，包括認知環境、社會環境以及社會政治環境、客觀物質環境等。
動態系統的特點是：
①系統的狀態變數是時間函式，即其狀態變數隨時間而變化。
②系統狀況由其狀態變數隨時間變化的信息來來描述。
③狀態變數的持續性。
研究現狀
在工程技術、經濟、自然科學和社會科學等領域中，普遍存在著許多隨時間而變化的複雜系統和非線性現象，如物價的波動、城市的擴展、天氣的變化人口的增長等人們通常需要根據動態系統的觀測數據建立合理的動態系統模型(動力學模型)，為系統分析、設計以及對系統未來狀態的預測提供依抵離散動態系統模型是一類非常重要的模型，但在建立模型的過程中，確定描述系統演化運動的動態方程組卻十分困難傳統的建模方法是憑直覺或經驗事先假定一組動態方程的結構，然後採用數值方法確定假定方程中的參數，但其合理性、精確性差及計算的煩瑣過程使傳統方法的套用受到一定限制，針對非線性多維高次的複雜系統建模確定方程的結構非常困難。遺傳規劃(簡稱GP)是在遺傳算法的基礎上發展起來的。它可以將結構估計與參數估計結合在一起，能夠在沒有完整的模型結構信息的情況下，利用觀測數據建立系統動態模型解決了遺傳算法不能描述層次化問題及缺乏動態可變性的缺點，為人們提供了複雜系統建模的一種新思路和新方法，目前在動態系統建模方面得到越來越廣泛地套用。遺傳規劃在離散動態系統建模中的套用，就是要解決離散動態系統的結構與關聯函式的建模。
系統描述
設一個動態系統由n個有關聯的狀態變數所描述，在離散時間步上對該系統進行觀測，從0-t時間步上的觀測數據為：
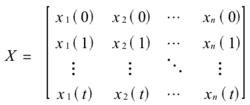離散動態系統其中，狀態變數間的關聯關係可以表示為如下動態方程組，xi(t)表示第i個狀態變數在t時間步上的狀態值。
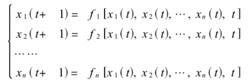離散動態系統記
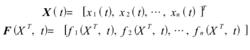離散動態系統則上式變換成：
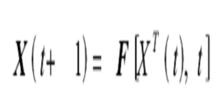離散動態系統離散動態系統建模就是求上式中的F，使得誤差最小。
魯棒控制概況
當控制系統中的某個物理量隨時間變化的規律不能用連續函式描述時，只在離散的時刻有數值，則這樣的系統稱為離散時間系統。
隨著計算機科學、脈衝技術、微處理器及數字元部件的發展，在生物、生態、航空、航天、經濟以及工程控制中的大量系統都需要用離散時間系統來描述。當連續時間系統在利用計算機對其進行分析和仿真時，也需將其離散化，然後再進行處理。
隨著系統理論研究領域的擴大和計算機技術的廣泛普及套用，離散控制系統理論得到迅速發展， 成為控制理論的重要組成部分。 離散系統理論在自動控制工程、通信、雷達技術、生物學、電力系統和核物理等領域發揮著重要的作用。
離散系統與連續系統的描述上有著本質的不同，但在分析研究方面又有著相似性，在連續時間續系統中的許多概念和研究方法，也可以推廣並套用於離散系統中。
在控制領域及各種工業生產過程中的多數系統，一般都難以建立精確的數學模型，有時即使得到了被控對象精確的數學模型，可是往往都是十分複雜的，利用已有的控制技術條件是難以處理的，因而需要對複雜的系統進行簡化處理；隨著在生產過程中元器件的磨損與老化，使得被控對象的性能也會發生變化，這就導致了我們所建立的數學模型和實際的被控對象之間存在著一定的偏差和不確定性，再加上現實生活中環境及各種條件的複雜與多樣，即存在著很多不確定的因素。因此研究具有不確定性的系統也具有重要的現實意義。
控制系統的魯棒性是指控制系統在某種類型的擾動作用下，包括自身模型的擾動下，系統某個性能指標保持不變的能力。系統具有良好的魯棒性是系統正常工作的保障。
穩定問題
追溯至1981年，中國學者鄧聚龍教授首創了灰色系統理論，在國際上引起了極大重視，並逐漸發展成為最常用的一種不確定系統的研究方法。研究灰色離散系統的漸近穩定性，可轉化為區間矩陣的離散穩定性。對於這一領域的研究，取得了一些成果，周朝順、鄧聚龍(1988)利用一般離散系統的Lyapunov方程給出了灰色離散系統的穩定性的充分判據，從而使灰色連續控制系統的研究擴展到了灰色離散系統;彭曉林、羅曉(1991)提出了區間矩陣離散穩定性的概念，並結合矩陣理論方法給出了灰色離散系統穩定與不穩定的代數判據，並將其一些結論套用到區間矩陣的連續上去；黃廷祝等(1999)用特殊矩陣分析方法和技術，用矩陣的元素獲得了該系統漸近穩定的簡單實用的充分條件，較以往的結果有較小的保守性，並使得特殊矩陣理論在其上得到充分的運用，許多己有的好的結論都可以轉化過來；韓金舫等(2004)運用矩陣特徵值分析技巧給出了一般區間矩陣及離散動態系統穩定、不穩定和混合穩定的簡捷判據.其中包含了充分條件，必要條件與充要條件，並修正了彭曉林的某些主要結論；劉建州、張月朗和方慶霞等(2007)用特殊矩陣分析方法得到了該系統漸近穩定的充分判據，推廣了前人的結果。
上述離散動態系統的不穩定性問題也可化為區間矩陣的不穩定性問題。彭曉林，羅曉(1991)提出了區間矩陣的不穩定性和離散動態系統的不穩定性概念。對於離散動態系統的不穩定性問題，彭曉林，羅曉結合矩陣理論和Gersehgorin圓盤定理給出了一些不穩定的代數判據。韓金舫等(2004)在修正了彭曉林的某些結論後，運用矩陣特徵值分析技巧得到了一般區間矩陣及離散動態系統不穩定的判據，並提出了區間矩陣混合穩定和離散動態系統混合穩定的概念。
