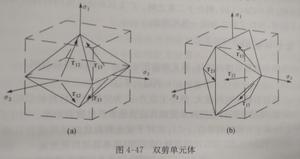
雙剪強度簡介
定義:當作用於單元體上的最大主剪應力和中間主剪應力的函式達到某一臨界值時,材料發生屈服或破壞,其數學表達式為
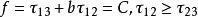 雙剪應力屈服模型
雙剪應力屈服模型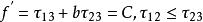 雙剪應力屈服模型
雙剪應力屈服模型式中,參數b可看做中間主剪應力對材料屈服的影響係數;C為材料的強度參數。
雙剪應力屈服模型概述
物體產生塑性變形的現象人們很早就已經發現,然而形成塑性理論並對其進行研究,則最早開始於1773年C.A.Coulomb提出土壤的屈服條件。1864年,法國工程師H.Tresca便最早把塑性力學的理論運用到金屬材料上,並公布了他做的關於衝壓和擠壓方面的一些實驗報告。根據實驗結果,他提出了最大剪應力屈服條件(即Tresca屈服條件),此屈服條件認為金屬材料在最大剪應力達到某一臨界值時就會發生塑性屈服。在此後的三十多年中,塑性力學並沒有得到太多的發展,基本上處於停滯狀態。直到二十世紀初期,Guest做了關於薄壁管的聯合拉伸和內壓實驗,其實驗結果證實了Tresca所提出的最大剪應力屈服條件後,塑性力學又重新開始迅速發展。此後二十年內很多人還進行了大量類似的實驗,並提出許多種屈服條件,其中最有影響的是M.Huber和R.VonMises從數學簡化上考慮所提出的屈服條件(即最大變形能屈服條件)。
Mohr—Coulomb屈服條件的本構模型
Tresca屈服條件和Mises屈服條件主要是對金屬材料成立的兩個屈服條件,但是這兩個屈服條件如果簡單地套用於岩土材料,會引起不可忽視的偏差。針對此,Mohr提出這樣一個假設:當材料某個平面上的剪應力達到某個極限值時,材料發生屈服。這也是一種剪應力屈服條件,但是與Tresca屈服條件不同,Mohr假設的這個極限值不是一個常數值,而是與該平面上的正應力有關,它可以表示為
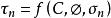 雙剪應力屈服模型
雙剪應力屈服模型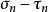 雙剪應力屈服模型
雙剪應力屈服模型上式中,C是材料粘聚強度,∅是材料的內摩擦角。這個函式關係式可以通過實驗確定。一般情況下,材料的內摩擦角隨著靜水應力的增加而逐漸減小,因而假定函式對應的曲線在 平面上呈雙曲線或拋物線或擺線。但在靜水應力不大的情況下,屈服曲線常用∅等於常數的直線來代替,它可以表示為
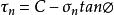 雙剪應力屈服模型
雙剪應力屈服模型上式就稱為Mohr—Coulomb屈服條件,即雙剪應力屈服模型的本構模型。
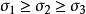 雙剪應力屈服模型
雙剪應力屈服模型設主應力大小次序為 ,則上式可以寫成用主應力表示的形式
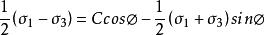 雙剪應力屈服模型
雙剪應力屈服模型三種本構模型的對比
Tresca,Mises,Mohr—Coulomb本構模型各有各的優缺點,它們在一定的條件下適合使用。
總的來講,在主應力大小已知的情況下,Tresca屈服條件套用起來比較方便,但是它有以下幾點缺點:
(1)在主應力大小未知的情況下,Tresca屈服條件不便使用;
(2)它忽略了中間主應力的影響;
(3)屈服曲線上有角點,給數學處理上帶來了困難。
Mises屈服條件克服了以上Tresca屈服條件的缺點,它的形式更簡單。在π平面上,如果我們規定在簡單拉伸時,兩種屈服條件重合,則Tresca六邊形將內接與Mises圓。兩種屈服條件都通過正六邊形的六個頂點,表明在單向應力狀態下兩者是一致的,但在純剪應力狀態下,兩者有最大差異。在純剪應力狀態下按Mises屈服條件確定的剪下屈服應力是由Tresca屈服條件計算的結果的1.155倍。
總體來說,Tresca屈服條件與Mises屈服條件主要是對金屬材料成立的兩個屈服條件,它們已經被金屬材料的實驗結果所證實。但是這兩個屈服條件卻不適合用在岩石、土和混凝土等一類的材料。因為實驗結果表明,這一類材料的性質與金屬材料的塑性性質有明顯的不同,主要反映在以下兩個方面。
(1)一般認為,金屬材料的體積變化是彈性的,無塑性體積變形。這對多數金屬在壓力不大的情況下是大致成立的。然而,對岩石、土和混凝土材料,實驗表明這類材料往往有塑性體積變形。
(2)金屬材料的屈服於淨水壓力無關,而這一類材料的屈服受到淨水壓力的影響很大。
因此,Tresca屈服條件和Mises屈服條件用在岩石、土和混凝土會引起不可忽視的偏差,而Mohr—Coulomb屈服條件能較好的適用於這類材料。由Mohr—Coulomb屈服條件的表達式知,如果不考慮材料內摩擦角的影響,即令∅=0,則有
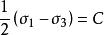 雙剪應力屈服模型
雙剪應力屈服模型這就是Tresca屈服條件。由此可見,Tresca屈服條件是Mohr—Coulomb屈服條件的推廣形式。